题目内容
7.函数y=xex(e为自然对数的底)在(1,f(1))点处的切线方程是( )| A. | y=2ex-e | B. | y=2ex-2e | C. | y=ex-e | D. | y=ex-1 |
分析 先求出切点的坐标,然后求出x=1处的导数,从而求出切线的斜率,利用点斜式方程即可求出切线方程.
解答 解:∵f(x)=xex,
∴f′(x)=ex+xex,∴f′(1)=2e,又f(1)=e,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y-e=2e(x-1),即y=2ex-e.
故选:A.
点评 本题主要考查了利用导数研究曲线上某点切线方程,考查导数的运用:求切线方程,主要考查导数的几何意义:函数在某点处的导数即为曲线在该点处切线的斜率,正确求导和运用点斜式方程是解题的关键,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
18.“函数y=f(x)在R上单调递增”是“f'(x)≥0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知命题p:?c>0,使方程x2-x+c=0有解,则¬p为( )
| A. | ?c>0,方程x2-x+c=0无解 | B. | ?c≤0,方程x2-x+c=0有解 | ||
| C. | ?c>0,使方程x2-x+c=0无解 | D. | ?c≤0,使方程x2-x+c=0有解 |
12.过抛物线C:y2=2px(p>0)的焦点且斜率为1的直线与C相交于A,B两点,若|AB|=4,则抛物线C的方程为( )
| A. | y2=x | B. | y2=2x | C. | y2=4x | D. | y2=8x |
16.若集合A={x|x2+x-6>0},集合B={x|-2<x<4},则A∩B等于( )
| A. | ∅ | B. | (-2,3) | C. | (3,4) | D. | (2,4) |
17.某几何体的三视图如图所示,则俯视图的面积为( )
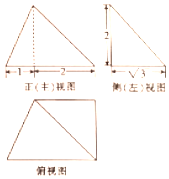

| A. | $5\sqrt{3}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | 5 | D. | $\frac{5}{2}$ |
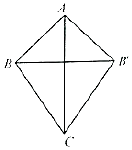 如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.
如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.