题目内容
4.设集合A={-2,-1,0,1,2},B={x|x2+2x<0},则A∩(∁RB)=( )| A. | {1,2} | B. | {0,1,2} | C. | {-2,1,2} | D. | {-2,0,1,2} |
分析 求出集合的等价条件,根据集合的基本运算进行求解即可.
解答 解:B={x|x2+2x<0}={x|-2<x<0},
则∁RB={x|x≥0或x≤-2},
则A∩(∁RB)={-2,0,1,2}
故选:D.
点评 本题主要考查集合的基本运算,求出不等式的等价条件是解决本题的关键.比较基础.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
14.已知全集U={x∈N|0<x<8},A={2,4,5},则∁UA=( )
| A. | {1,3,6,7} | B. | {2,4,6} | C. | {1,3,7,8} | D. | {1,3,6,8} |
15.已知命题p:?c>0,使方程x2-x+c=0有解,则¬p为( )
| A. | ?c>0,方程x2-x+c=0无解 | B. | ?c≤0,方程x2-x+c=0有解 | ||
| C. | ?c>0,使方程x2-x+c=0无解 | D. | ?c≤0,使方程x2-x+c=0有解 |
12.过抛物线C:y2=2px(p>0)的焦点且斜率为1的直线与C相交于A,B两点,若|AB|=4,则抛物线C的方程为( )
| A. | y2=x | B. | y2=2x | C. | y2=4x | D. | y2=8x |
9.设Sn是等比数列{an}的前n项和,公比q>0,则Sn+1an与Snan+1的大小关系是( )
| A. | Sn+1an>Snan+1 | B. | Sn+1an<Snan+1 | C. | Sn+1an≥Snan+1 | D. | Sn+1an≤Snan+1 |
16.若集合A={x|x2+x-6>0},集合B={x|-2<x<4},则A∩B等于( )
| A. | ∅ | B. | (-2,3) | C. | (3,4) | D. | (2,4) |
14.空间的点M(1,0,2)与点N(-1,2,0)的距离为( )
| A. | $2\sqrt{2}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | 4 |
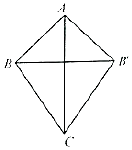 如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.
如图所示,在四边形ABCB'中,△ABC≌△AB'C,AB⊥AB',cos∠BCB'=$\frac{3}{4}$,BC=2$\sqrt{7}$,则△BCB'外接圆的面积为8π.