题目内容
4.求下列圆的方程(1)求过三点O(0,0),A(1,1),B(4,2)的圆的一般方程
(2)求圆心在直线y=-4x上,且与直线x+y-1=0相切于点P(3,-2)的圆的方程.
分析 (1)设所求圆的方程为x2+y2+Dx+Ey+F=0,将三点O(0,0)、A(1,1)、B(4,2)的坐标代入,解之可得D,E,F,的值.
(2)求出圆心与半径,即可求出圆的标准方程,并化为圆的一般方程.
解答 解:设所求圆的方程为x2+y2+Dx+Ey+F=0,由O、A、B在圆上,则有$\left\{\begin{array}{l}{F=0}\\{D+E+F+2=0}\\{4D+2E+F+20=0}\end{array}\right.$,
解得:D=-8,E=6,F=0,
故所求圆的方程为x2+y2-8x+6y=0;
(2)过切点且与l:x+y-1=0垂直的直线为y=x-5,与y=-4x联立可求得圆心为(1,-4),
∴半径r=$\sqrt{(1-3)^{2}+(-4+2)^{2}}$=2$\sqrt{2}$,
∴所求圆的方程为(x-1)2+(y+4)2=8.
点评 本题考查圆的一般方程与标准方程,考查直线与圆的位置关系,考查解方程组的能力,属于中档题.

练习册系列答案
相关题目
14.设函数$f(x)=\frac{f'(1)}{e}•{e^x}-f(0)x+\frac{1}{2}{x^2}$,则曲线f(x)在点(1,f(1))处切线方程为( )
| A. | $y=\frac{1}{e}x-\frac{1}{2}$ | B. | $y=ex-\frac{1}{2}$ | C. | $y=-\frac{1}{e}x+\frac{1}{2}$ | D. | $y=ex+\frac{1}{2}$ |
15.如图所示,某空间几何体的正视图与侧视图相同,则此几何体的表面积为( )
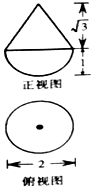

| A. | 6π | B. | $\frac{2π}{3}+\sqrt{3}$ | C. | 4π | D. | $2π+\sqrt{3}$ |
12.抛物线y2=12x上与焦点的距离等于7的点的横坐标是( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
19.为了得到函数$y=4sin(2x+\frac{π}{5}),x∈R$的图象,只需把函数$y=4sin(x+\frac{π}{5}),x∈R$的图象上所有点的( )
| A. | 横坐标伸长到原来的2倍,纵坐标不变 | |
| B. | 纵坐标伸长到原来的2倍,横坐标不变 | |
| C. | 横坐标伸长到原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 纵坐标伸长到原来的$\frac{1}{2}$倍,横坐标不变 |
9.已知某个几何体的三视图如图所示,图中每个小正方形的边长为1,则该几何体的表面积为( )


| A. | 4+4$\sqrt{2}$ | B. | 8+4$\sqrt{2}$ | C. | 8+2$\sqrt{3}$ | D. | 8+4$\sqrt{3}$ |
16.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )


| A. | 32+8π | B. | 32+$\frac{8π}{3}$ | C. | 16+$\frac{8π}{3}$ | D. | 16+8π |
4.设集合M={x|x-x2=0},N={x|ln(1-x)<0},则M∪N=( )
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (∞,1] |