题目内容
3.若函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象关于坐标原点中心对称,且在y轴右侧的第一个极值点为x=$\frac{π}{3}$,则函数f(x)的最小正周期为$\frac{4π}{3}$.分析 由条件利用正弦函数的图象的特征,正弦函数的奇偶性、最值、周期性,求得函数f(x)的最小正周期.
解答 解:函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象关于坐标原点中心对称,可得φ=0,
∵f(x)在y轴右侧的第一个极值点为x=$\frac{π}{3}$,∴ω•$\frac{π}{3}$=$\frac{π}{2}$,∴ω=$\frac{3}{2}$,∴函数f(x)=Asin($\frac{3}{2}$x),
则函数f(x)的最小正周期为$\frac{2π}{\frac{3}{2}}$=$\frac{4π}{3}$,
故答案为:$\frac{4}{3}π$.
点评 本题主要考查正弦函数的图象的特征,正弦函数的奇偶性、最值、周期性,属于基础题.

练习册系列答案
相关题目
14.若m<0,则直线2mx-m2y-y+3=0的倾斜角的范围是( )
| A. | [0,$\frac{π}{4}$] | B. | [$\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$] | D. | [$\frac{3π}{4}$,π) |
15.已知x、y满足不等式组$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ 4x+3y≤14\end{array}$,设(x+2)2+(y+1)2的最小值为ω,则函数f(t)=sin(ωt+$\frac{π}{6}$)的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{5}$ |
12.若函数f(x)=sinωx+cosωx(ω>0)的图象相邻两条对称轴之间的距离为3,则ω值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
13.将函数y=4sin(4x+$\frac{π}{6}$)的图象上各点的横坐标伸长为原来的2倍,再向右平移$\frac{π}{6}$个单位,所得函数图象的一个对称中心为( )
| A. | $(\frac{13π}{48},0)$ | B. | $(\frac{π}{8},0)$ | C. | $(\frac{5π}{8},0)$ | D. | $(\frac{7π}{12},0)$ |
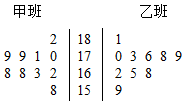 从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.
从某中学的甲乙两个班中各随机抽取10名同学,分别测量他们的身高(单位:cm),得到身高数据的茎叶图如图所示,若从乙班被抽取的这10名同学中再随机抽取2名身高不低于173cm的同学,则身高为176cm的同学被抽到的概率为$\frac{2}{5}$.