题目内容
15.已知x、y满足不等式组$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ 4x+3y≤14\end{array}$,设(x+2)2+(y+1)2的最小值为ω,则函数f(t)=sin(ωt+$\frac{π}{6}$)的最小正周期为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{5}$ |
分析 作出不等式组对应的平面区域,利用,(x+2)2+(y+1)2的几何意义求出ω的值,然后根据三角函数的周期公式进行求解即可.
解答  解:作出不等式组对应的平面区域,(x+2)2+(y+1)2的几何意义是区域内的点到定点C(-2,-1)的距离的平方
解:作出不等式组对应的平面区域,(x+2)2+(y+1)2的几何意义是区域内的点到定点C(-2,-1)的距离的平方
由图象知OC的距离最小,
此时最小值为ω=(0+2)2+(0+1)2=4+1=5,
f(t)=sin(5t+$\frac{π}{6}$),
则最小正周期T=$\frac{2π}{5}$,
故选:D.
点评 本题主要考查三角函数周期的计算以及线性规划的应用,根据线性规划的知识求出ω的值是解决本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
6.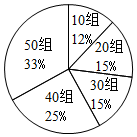 “我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
“我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
10组:12-19岁
20组:20-29岁
30组:30-39岁
40组:40-49岁
50组:50岁以上
在某歌手演唱完一首民族歌曲后,得票情况如图所示:
已知该歌手共获得了215张选票.
(1)完成2×2列联表:
(2)判断是否有99%的把握认为投票与否和年龄有关,说明你的理由.(下面的临界值表供参考)
(参考公式x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$,n=n1++n2++n+1+n+2)
(3)以上图中投票情况,从20组和40组中随机各抽取1人,求其中投票的人数ξ的分布列及其期望.
 “我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
“我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:10组:12-19岁
20组:20-29岁
30组:30-39岁
40组:40-49岁
50组:50岁以上
在某歌手演唱完一首民族歌曲后,得票情况如图所示:
已知该歌手共获得了215张选票.
(1)完成2×2列联表:
| 投票 年龄 | 是 | 否 | 合计 |
| 10组 | |||
| 50组 | |||
| 合计 |
| P(x2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(3)以上图中投票情况,从20组和40组中随机各抽取1人,求其中投票的人数ξ的分布列及其期望.
10.设实数x,y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{y≥x-1}\\{y≤5-2x}\end{array}\right.$,(2,1)是目标函数z=-ax+y取最大值的唯一最优解,则实数a的取值范围是( )
| A. | (0,1) | B. | (0,1] | C. | (-∞,-2) | D. | (-∞,-2] |
 将3种作物全部种植在如图的5块试验田里,每块试验田种植一种作物且相邻的试验田不能种植同一种作物,则共有多少种种植方法?
将3种作物全部种植在如图的5块试验田里,每块试验田种植一种作物且相邻的试验田不能种植同一种作物,则共有多少种种植方法?