题目内容
14.若m<0,则直线2mx-m2y-y+3=0的倾斜角的范围是( )| A. | [0,$\frac{π}{4}$] | B. | [$\frac{π}{4}$,$\frac{π}{2}$) | C. | ($\frac{π}{2}$,$\frac{3π}{4}$] | D. | [$\frac{3π}{4}$,π) |
分析 化直线的一般式方程为斜截式,利用基本不等式求出斜率的范围,则直线倾斜角的范围可求.
解答 解:由2mx-m2y-y+3=0,得$y=\frac{2m}{{m}^{2}+1}x+\frac{3}{{m}^{2}+1}$,
∴直线的斜率k=$\frac{2m}{{m}^{2}+1}=\frac{2}{m+\frac{1}{m}}$,
∵m<0,
∴$m+\frac{1}{m}=-[(-m)+\frac{1}{-m}]≤-2\sqrt{(-m)(-\frac{1}{m})}$=-2.
∴k=$\frac{2}{m+\frac{1}{m}}$∈[-1,0).
设直线2mx-m2y-y+3=0的倾斜角为θ(0≤θ<π),
∴-1≤tanθ<0,则θ∈[$\frac{3π}{4},π$).
故选:D.
点评 本题考查直线的倾斜角,考查了直线的倾斜角和斜率的关系,训练了利用基本不等式求最值,是中档题.

练习册系列答案
相关题目
2.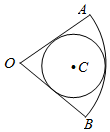 如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
 如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )
如图,圆C内切于扇形AOB,∠AOB=$\frac{π}{3}$,若向扇形AOB内随机投掷300个点,则落入圆内的点的个数估计值为( )| A. | 450 | B. | 400 | C. | 200 | D. | 100 |
19.若实数x,y满足约束条件$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{4x-y+1≥0}\end{array}\right.$则目标函数z=$\frac{y+1}{x+3}$的最大值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
6.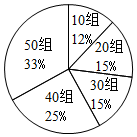 “我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
“我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
10组:12-19岁
20组:20-29岁
30组:30-39岁
40组:40-49岁
50组:50岁以上
在某歌手演唱完一首民族歌曲后,得票情况如图所示:
已知该歌手共获得了215张选票.
(1)完成2×2列联表:
(2)判断是否有99%的把握认为投票与否和年龄有关,说明你的理由.(下面的临界值表供参考)
(参考公式x2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$,n=n1++n2++n+1+n+2)
(3)以上图中投票情况,从20组和40组中随机各抽取1人,求其中投票的人数ξ的分布列及其期望.
 “我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:
“我是歌手”是芒果卫视推出的节目,其中歌手由大众评审打分,已知大众评审有五个年龄层,每组100人,共500人.年龄层分布知如下:10组:12-19岁
20组:20-29岁
30组:30-39岁
40组:40-49岁
50组:50岁以上
在某歌手演唱完一首民族歌曲后,得票情况如图所示:
已知该歌手共获得了215张选票.
(1)完成2×2列联表:
| 投票 年龄 | 是 | 否 | 合计 |
| 10组 | |||
| 50组 | |||
| 合计 |
| P(x2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(3)以上图中投票情况,从20组和40组中随机各抽取1人,求其中投票的人数ξ的分布列及其期望.