题目内容
6.某企业有甲、乙两个研发小组,他们研发新产品成功的概率分别为$\frac{2}{3}$和$\frac{3}{5}$.现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立,则至少有一种新产品研发成功的概率为$\frac{13}{15}$.分析 利用对立事件的概率公式,计算即可,
解答 解:设至少有一种新产品研发成功的事件为事件A且事件B为事件A的对立事件,则事件B为一种新产品都没有成功,
因为甲乙研发新产品成功的概率分别为$\frac{2}{3}$和$\frac{3}{5}$.
则P(B)=(1-$\frac{2}{3}$)(1-$\frac{3}{5}$)=$\frac{2}{15}$,
再根据对立事件的概率之间的公式可得P(A)=1-P(B)=$\frac{13}{15}$,
故至少有一种新产品研发成功的概率$\frac{13}{15}$.
故答案为$\frac{13}{15}$.
点评 本题主要考查了对立事件的概率,考查学生的计算能力,比较基础.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
16.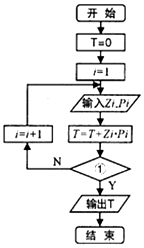 某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率
某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率
 某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率
某校为了了解高三学生日平均睡眠时间(单位:h),随机选择了50位学生进行调查.下表是这50位同学睡眠时间的频率分布表:(1)根据所给数据,求众数和中位数;(2)现根据如下算法流程图用计算机统计平均睡眠时间,则判断框①中应填入什么条件?(3)若从第1组和第5组中随机取出2个数据,求相应的两个同学的睡眠时间差的绝对值大于1小时的概率| 组别(i) | 睡眠时间 | 组中值(Zi) | 频数 | 频率(Pi) |
| 1 | [4.5,5.5) | 5 | 2 | 0.04 |
| 2 | [5.5,6.5) | 6 | 6 | 0.12 |
| 3 | [6.5,7.5) | 7 | 20 | 0.40 |
| 4 | [7.5,8.5) | 8 | 18 | 0.36 |
| 5 | [8.5,9.5) | 9 | 3 | 0.06 |
| 6 | [9.5,10.5) | 10 | 1 | 0.02 |
15.设函数$f(x)=({{x^2}-2x})lnx+({a-\frac{1}{2}}){x^2}+2({1-a})x+a$.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当a<-2时,讨论f(x)的零点个数.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当a<-2时,讨论f(x)的零点个数.
16.若存在两个正数x,y,使得等式${x^2}•{e^{\frac{y}{x}}}-2a{y^2}=0$成立,其中e为自然对数的底数,则实数a的取值范围是( )
| A. | $[{\frac{e^2}{8},+∞})$ | B. | $({0,\frac{e^3}{27}}]$ | C. | $[{\frac{e^3}{27},+∞})$ | D. | $({0,\frac{e^2}{8}}]$ |
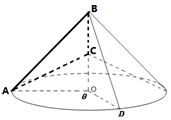 如图,等腰Rt△AOB,OA=OB=2,点C是OB的中点,△AOB绕BO所在的边逆时针旋转一周.
如图,等腰Rt△AOB,OA=OB=2,点C是OB的中点,△AOB绕BO所在的边逆时针旋转一周.