题目内容
已知f（x-3）=x2+2x+1，则f（x+3）的表达式为： ．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：本题可以先用换元法求出函数f（t）的解析式，再令t=x+3，得到f（x+3）的表达式，得到本题结论．
解答：
解：∵函数f（x-3）=x2+2x+1，
∴令x-3=t，则x=t+3，
∴f（t）=（t+3）2+2（t+3）+1，
∴f（t）=t2+8t+16．
令t=x+3，
则有：f（x+3）=（x+3）2+8（x+3）+16
=x2+14x+49．
故答案为：f（x+3）=x2+14x+49．
∴令x-3=t，则x=t+3，
∴f（t）=（t+3）2+2（t+3）+1，
∴f（t）=t2+8t+16．
令t=x+3，
则有：f（x+3）=（x+3）2+8（x+3）+16
=x2+14x+49．
故答案为：f（x+3）=x2+14x+49．
点评：本题考查了求函数的解析式，本题难度不大，属于基础题．
练习册系列答案
相关题目
根式
（式中a＞0）的分数指数幂形式为（ ）
|
A、a-
| ||
B、a
| ||
C、a-
| ||
D、a
|
若{1，a，
}={0，a2，a+b}，则a2013+b2012的值为（ ）
| b |
| a |
| A、0 | B、1 | C、±1 | D、-1 |
如图，在正四面体A-BCD中，E为棱AD的中点，则CE与平面BCD的夹角的正弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
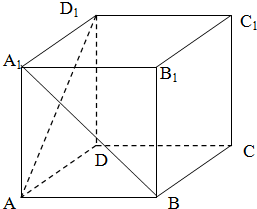已知正方体ABCD-A1B1C1D1，求：
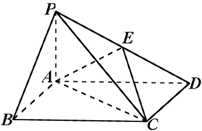如图，四棱锥P-ABCD中，底面ABCD为是矩形，PA⊥底面ABCD，E为棱PD的中点，AP=2，AD=3，且三棱锥E-ACD的体积为1．