题目内容
16.已知数列{an}的首项a1=1,且满足an+1-an≤2n,an-an+2≤-3×2n,则a2017=22017-1.分析 an+1-an≤2n,可得an+2-an+1≤2n+1,又an-an+2≤-3×2n,可得an+1-an≥2n,于是an+1-an=2n,再利用“累加求和”方法即可得出.
解答 解:∵an+1-an≤2n,
∴an+2-an+1≤2n+1,又an-an+2≤-3×2n,∴an+1-an≥2n,
∴2n≤an+1-an≤2n,
∴an+1-an=2n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n-1+2n-1+…+2+1
=$\frac{{2}^{n}-1}{2-1}$=2n-1.
∴a2017=22017-1.
故答案为:22017-1
点评 本题考查了递推关系、不等式的性质、“累加求和”方法、等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设集合A={x|-a<x<a},其中a>0,命题p:1∈A,命题q:2∈A,若p∨q为真命题,p∧q为假命题,则a的取值范围是( )
| A. | 0<a<1或a>2 | B. | 0<a<1或a≥2 | C. | 1<a≤2 | D. | 1≤a≤2 |
4.已知实数x,y满足$\left\{\begin{array}{l}{|x-y|≤1}\\{|x+y|≤3}\end{array}\right.$,则|3x+y|的最大值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
11.在正项等比数列{an}中,a1008a1010=$\frac{1}{100}$,则lga1+lga2+…+lga2017=( )
| A. | -2016 | B. | -2017 | C. | 2016 | D. | 2017 |
1.下列函数中满足在(-∞,0)上单调递减的偶函数是( )
| A. | $y={({\frac{1}{2}})^{|x|}}$ | B. | y=|log2(-x)| | C. | $y={x^{\frac{2}{3}}}$ | D. | y=sin|x| |
8.已知命题p,q,“¬p为假”是“p∨q为真”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.若($\sqrt{x}$+$\frac{2}{{x}^{2}}$)n展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
| A. | 90 | B. | 45 | C. | 120 | D. | 180 |
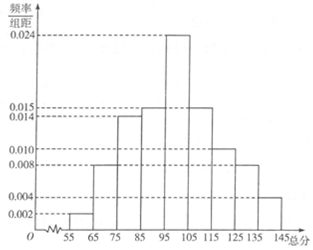 某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.
某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.