题目内容
在△ABC中，若c=2，a+b=7，cosA=-
，则b= ．
| 1 |
| 4 |
考点：余弦定理
专题：解三角形
分析：利用余弦定理列出关系式，将c，a=7-b，cosA的值代入即可求出b的值．
解答：
解：∵在△ABC中，c=2，a+b=7，即a=7-b，cosA=-
，
∴由余弦定理得：a2=b2+c2-2bccosA，即（7-b）2=b2+4+b，
整理得：49-14b+b2=b2+4+b，即15b=45，
解得：b=3．
故答案为：3
| 1 |
| 4 |
∴由余弦定理得：a2=b2+c2-2bccosA，即（7-b）2=b2+4+b，
整理得：49-14b+b2=b2+4+b，即15b=45，
解得：b=3．
故答案为：3
点评：此题考查了余弦定理，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
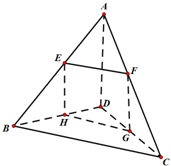空间四边形ABCD中，AD=BC=a，与直线AD，BC都平行的平面分别交AB，AC，CD，BD于E，F，H．