题目内容
已知定义在实数集R上的函数f(x)满足f(1)=1,且f(x)的导数f′(x)在R上恒有f′(x)<
,则不等式f(x)<
+
的解集为 .
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
考点:一元二次不等式的解法
专题:函数思想,导数的概念及应用
分析:构造函数g(x)=f(x)-(
x+
),x∈R;
利用g′(x)判定g(x)的单调性,从而求出不等式f(x)<
x+
的解集.
| 1 |
| 2 |
| 1 |
| 2 |
利用g′(x)判定g(x)的单调性,从而求出不等式f(x)<
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:根据题意,设g(x)=f(x)-(
x+
),x∈R;
∴g′(x)=f′(x)-
<0,
∴g(x)在R上是单调减函数;
又∵g(1)=f(1)-(
+
)=0,
∴当x>1时,g(x)<0恒成立,
即f(x)<
x+
在x>1时恒成立,
∴原不等式的解集是(1,+∞).
故答案为:(1,+∞).
| 1 |
| 2 |
| 1 |
| 2 |
∴g′(x)=f′(x)-
| 1 |
| 2 |
∴g(x)在R上是单调减函数;
又∵g(1)=f(1)-(
| 1 |
| 2 |
| 1 |
| 2 |
∴当x>1时,g(x)<0恒成立,
即f(x)<
| 1 |
| 2 |
| 1 |
| 2 |
∴原不等式的解集是(1,+∞).
故答案为:(1,+∞).
点评:本题考查了求不等式的解集的问题,解题时应构造函数,由导数判定函数的单调性并求出不等式的解集,
是基础题目.
是基础题目.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
以下是解决数学问题的思维过程的流程图:
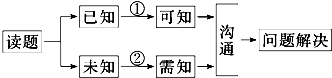
在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )

在此流程图中,①②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
| A、①-综合法,②-分析法 |
| B、①-分析法,②-综合法 |
| C、①-综合法,②-反证法 |
| D、①-分析法,②-反证法 |
 如图所示,点A,B是圆O上的两点,∠AOB=120°,点D是圆周上异于A,B的任意一点,线段OD与线段AB交于点C.若
如图所示,点A,B是圆O上的两点,∠AOB=120°,点D是圆周上异于A,B的任意一点,线段OD与线段AB交于点C.若