题目内容
求圆心在直线y=2x上,且经过点(2,-1),与直线x+y=1相切的圆的方程.
考点:圆的切线方程
专题:计算题,直线与圆
分析:设出圆心的坐标为(a,2a),利用两点间的距离公式表示出圆心到A的距离即为圆的半径,且根据圆与直线x+y=1相切,根据圆心到直线的距离等于圆的半径列出关于a的方程,求出方程的解得到a的值,确定出圆心坐标,进而求出圆的半径,根据圆心和半径写出圆的标准方程即可.
解答:
解:设所求圆心坐标为(a,2a)
由条件得
=
,化简得a2+6a+9=0,
∴a=-3,
∴圆心为(-3,-6),半径r=5
,
∴所求圆方程为(x+3)2+(y+6)2=50.
由条件得
| (a-2)2+(2a+1)2 |
| |a+2a-1| | ||
|
∴a=-3,
∴圆心为(-3,-6),半径r=5
| 2 |
∴所求圆方程为(x+3)2+(y+6)2=50.
点评:本题考查了直线与圆的位置关系,涉及的知识有两点间的距离公式,点到直线的距离公式,圆的标准方程,当直线与圆相切时,圆心到直线的距离等于圆的半径,常常利用此性质列出方程来解决问题.

练习册系列答案
相关题目
直线在平面外是指( )
| A、直线与平面没有公共点 |
| B、直线与平面相交 |
| C、直线与平面平行 |
| D、直线与平面最多只有一个公共点 |
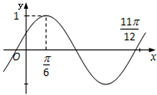 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、y=sin(2x+
| ||
B、y=sin(2x-
| ||
C、y=cos(2x+
| ||
D、y=cos(2x-
|
已知△ABC三个顶点在同一个球面上,∠BAC=90°,AB=AC=2,若球心到平面ABC距离为1,则该球体积为( )
A、2
| ||
B、4
| ||
C、6
| ||
D、8
|
 为了了解某班在全市“一检”中数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生的试卷成绩作为样本,他们数学成绩的茎叶图如图所示,其中茎为百位数和十位数,叶为个位数.
为了了解某班在全市“一检”中数学成绩的情况,按照分层抽样分别抽取了10名男生和5名女生的试卷成绩作为样本,他们数学成绩的茎叶图如图所示,其中茎为百位数和十位数,叶为个位数.