题目内容
若集合A={x|3x2-4x+1＜0}，集合B={x|
＞1}，则A∪B=（ ）
| 1 |
| x |
A、（
| ||
| B、（0，1） | ||
| C、（-∞，1） | ||
D、（0，
|
考点：并集及其运算
专题：集合
分析：分别求解二次不等式和分式不等式化简集合A，B，然后直接利用并集概念得答案．
解答：
解：A={x|3x2-4x+1＜0}={x|
＜x＜1}，
B={x|
＞1}={x|0＜x＜1}，
则A∪B={x|
＜x＜1}∪{x|0＜x＜1}=（0，1）．
故选：B．
| 1 |
| 3 |
B={x|
| 1 |
| x |
则A∪B={x|
| 1 |
| 3 |
故选：B．
点评：本题考查了并集及其运算，考查了二次不等式和分式不等式的解法，是基础题．
练习册系列答案
相关题目
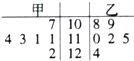某质检机构检测某产品的质量是否合格，在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品，称其质量（单位：克），分别记录抽查数据，获得质量数据茎叶图（如图）．
如图，已知正四棱锥P-ABCD，AB=6，PA=5，求外接球与内切球的半径R．