题目内容
已知圆心为C的圆经过点A(-1,1)和B(-2,-2),且圆心在直线l:x+y-1=0上.
(1)求圆心为C的圆的标准方程;
(2)设点P在圆C上,点Q在直线x-y+5=0上,求PQ的最小值;
(3)若直线kx-y+5=0被圆C所截得弦长为8,求k的值.
(1)求圆心为C的圆的标准方程;
(2)设点P在圆C上,点Q在直线x-y+5=0上,求PQ的最小值;
(3)若直线kx-y+5=0被圆C所截得弦长为8,求k的值.
考点:直线与圆相交的性质,圆的标准方程
专题:计算题,直线与圆
分析:(1)根据题意设出圆的标准方程为(x-a)2+(y-b)2=r2,得到圆心坐标为(a,b),半径为r,将A与B坐标代入圆方程,消去r得到关于a与b的方程,再将圆心坐标代入x+y-1=0中得到关于a与b的方程,联立求出a与b的值,确定出r的值,即可确定出圆的方程.
(2)由题意求出圆心到直线的距离,减去圆的半径即可得到|PQ|的最小值.
(3)由圆的半径,弦长,利用垂径定理及勾股定理求出弦心距d的值,再由圆心C坐标和直线kx-y+5=0,利用点到直线的距离公式列出关于k的方程,求出方程的解即可得到k的值.
(2)由题意求出圆心到直线的距离,减去圆的半径即可得到|PQ|的最小值.
(3)由圆的半径,弦长,利用垂径定理及勾股定理求出弦心距d的值,再由圆心C坐标和直线kx-y+5=0,利用点到直线的距离公式列出关于k的方程,求出方程的解即可得到k的值.
解答:
(1)解:设圆的标准方程为(x-a)2+(y-b)2=r2,得到圆心坐标为(a,b),半径为r,
将A与B坐标代入圆方程得:(-1-a)2+(1-b)2=r2,(-2-a)2+(-2-b)2=r2,
消去r,整理得:a+3b+3=0①,
将圆心坐标代入x+y-1=0得:a+b-1=0②,
联立①②解得:a=3,b=-2,r2=(-1-3)2+(1+2)2=25,
则圆C的标准方程为(x-3)2+(y+2)2=25.
(2)解:由于圆C:(x-3)2+(y+2)2=25,
则C(3,-2),半径r为:5,
由于C(3,-2)到直线l:x-y+5=0的距离为:
=5
,
故|PQ|的最小值是:5
-5.
(3)解:∵圆C半径为5,弦长为8,
∴圆心到直线kx-y+5=0的距离d=
=3,即
=3,
解得:k=-
.
将A与B坐标代入圆方程得:(-1-a)2+(1-b)2=r2,(-2-a)2+(-2-b)2=r2,
消去r,整理得:a+3b+3=0①,
将圆心坐标代入x+y-1=0得:a+b-1=0②,
联立①②解得:a=3,b=-2,r2=(-1-3)2+(1+2)2=25,
则圆C的标准方程为(x-3)2+(y+2)2=25.
(2)解:由于圆C:(x-3)2+(y+2)2=25,
则C(3,-2),半径r为:5,
由于C(3,-2)到直线l:x-y+5=0的距离为:
| |3+2+5| | ||
|
| 2 |
故|PQ|的最小值是:5
| 2 |
(3)解:∵圆C半径为5,弦长为8,
∴圆心到直线kx-y+5=0的距离d=
| 52-42 |
| |3k+7| | ||
|
解得:k=-
| 20 |
| 21 |
点评:本题考查了直线与圆的位置关系,涉及的知识有:二元一次方程组的解法,以及圆的标准方程,求出圆心坐标与半径是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
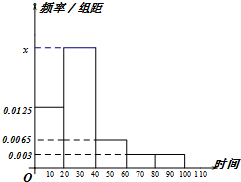 某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].