题目内容
某四面体的三视图都为直角三角形,如图所示,则该四面体的体积是( )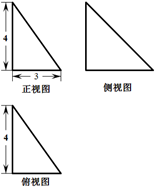
A. | B. | C. | D. |
B
解析试题分析:由三视图知:该几何体为三棱锥,三棱锥的底面是直角三角形,两直角边为3和4,三棱锥的高为4,所以该几何体的体积为: 。
。
考点:三视图;棱锥的体积公式。
点评:解决这类题的关键是准确分析出几何体的结构特征,发挥自己的空间想象力,把立体图形和平面图形进行对照,找出几何体中的数量关系。

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
在正四面体 中,点
中,点 分别是
分别是 的中点,则下面四个结论不成立的是( )
的中点,则下面四个结论不成立的是( )
| A.BC∥平面PDF | B. |
C. | D. |
已知平面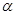 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与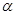 成
成 角的平面
角的平面 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4 、13
、13 ,则球面面积为
,则球面面积为
A.36 | B.48 | C.64 | D.100 |
球的表面积与它的内接正方体的表面积之比是( )
A.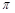 | B. |
C. | D. |
某几何体的三视图及其相应的度量信息如图所示,则该几何体的表面积为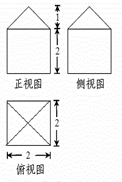
A.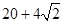 | B. | C.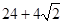 | D.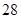 |
一空间几何体的三视图如图,则该几何体的体积为( )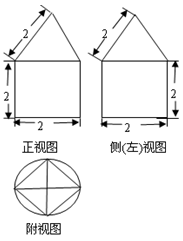
A.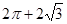 | B.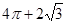 |
C.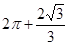 | D.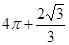 |

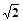
 的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为
的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为







