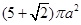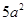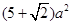题目内容
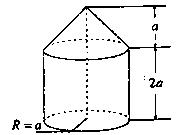
某几何体的三视图及其相应的度量信息如图所示,则该几何体的表面积为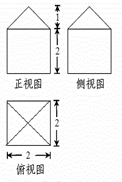
A.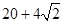 | B. | C.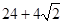 | D.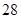 |
A
解析试题分析:根据题意可知,该几何体是四棱锥和四棱柱的简单组合体,那么可知四棱柱的底面为正方形,边长为2,高为2,而棱锥的高为1,那么可知几何体的表面积公式为 ,故答案为A.
,故答案为A.
考点:三视图,几何体的表面积
点评:根据三视图还原几何体是解决该试题的关键,然后利用度量关系得到对应的长度,属于基础题。

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知三棱锥的底面是边长为 的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为
的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为
A. | B. | C. | D. |
某四面体的三视图都为直角三角形,如图所示,则该四面体的体积是( )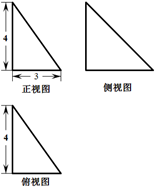
A. | B. | C. | D. |
一个几何体的三视图如图所示,则该几何体的体积为( )
| A.25 | B.36 | C.12 | D.24 |
棱长为1的正方体的外接球的表面积为
A. | B. | C. | D. |
已知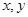 满足
满足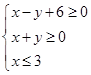 ,若
,若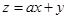 的最大值为
的最大值为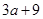 ,最小值为
,最小值为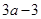 ,则a的范围为 ( )
,则a的范围为 ( )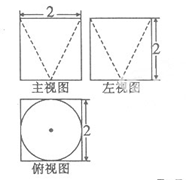
A.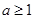 | B.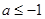 | C.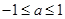 | D.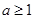 或 或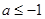 |
右图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧视图的面积为( )
A.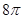 | B.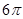 | C.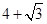 | D.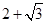 |