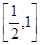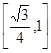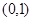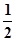题目内容
已知平面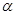 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与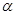 成
成 角的平面
角的平面 截该球面得圆N若圆M、圆N面积分别为4
截该球面得圆N若圆M、圆N面积分别为4 、13
、13 ,则球面面积为
,则球面面积为
A.36 | B.48 | C.64 | D.100 |
C
解析试题分析:圆M的面积为4π∴圆M的半径为2
根据勾股定理可知OM= ,∵圆N的面积为13π
,∵圆N的面积为13π
∴圆N的半径为 根据勾股定理可知ON=
根据勾股定理可知ON= ∵过圆心M且与α成
∵过圆心M且与α成 二面角的平面β截该球面得圆N,∴∠OMN=30°,在直角三角形OMN中,OM="2ON.," 2
二面角的平面β截该球面得圆N,∴∠OMN=30°,在直角三角形OMN中,OM="2ON.," 2 =
= ,R=4,可知球的表面积为64
,R=4,可知球的表面积为64 ,故选C.
,故选C.
考点:球内接多面体,球的体积和表面积
点评:本题主要考查了二面角的平面角,以及解三角形知识,同时考查空间想象能力,分析问题解决问题的能力,属于中档题.

练习册系列答案
相关题目
设 是两条直线,
是两条直线, 是两个平面,则
是两个平面,则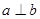 的一个充分条件是( )
的一个充分条件是( )
A.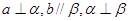 | B.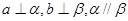 |
C.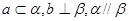 | D.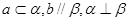 |
已知三棱锥的底面是边长为 的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为
的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为
A. | B. | C. | D. |
如图是一个正三棱柱体的三视图,该柱体的体积等于
A. | B.2 | C.2 | D. |
某四面体的三视图都为直角三角形,如图所示,则该四面体的体积是( )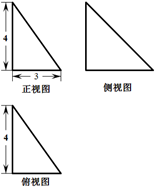
A. | B. | C. | D. |
已知圆锥的底面半径为1,且它的侧面展开图是一个半圆,则这个圆锥的体积为( )
A.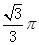 | B.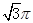 | C.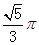  | D.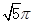 |
 内的射影构成的图形面积的取值范围是( )
内的射影构成的图形面积的取值范围是( )