题目内容
10．已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{3}$，且b≠d，则$\frac{a-c}{b-d}$=（ ）| A． | $\frac{2}{3}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{1}{5}$ |
分析 利用已知条件列出关系式，求解即可．
解答 解：$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{3}$，且b≠d，可得a=$\frac{2}{3}$b，c=$\frac{2}{3}$d，
$\frac{a-c}{b-d}$=$\frac{\frac{2}{3}（b-d）}{b-d}$=$\frac{2}{3}$．
故选：A．
点评 本题考查代数式的值的求法，考查计算能力．
练习册系列答案
相关题目
5．若$\sqrt{4-{a}^{2}}$=$\sqrt{{a}^{2}-4}$，则a的值为（ ）
| A． | 0 | B． | ±2 | C． | ±4 | D． | 2 |
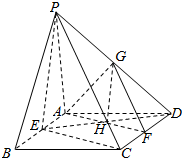如图，四棱锥P-ABCD的底面是平行四边形，PA=PB=AB=2，E，F分别是AB，CD的中点，平面AGF∥平面PEC，PD∩平面AGF=G，ED与AF相交于点H，则GH=$\frac{\sqrt{3}}{2}$．