题目内容
6.已知点P是函数y=sin(2x+α)图象与x轴的一个交点,A,B为P点右侧距离点P最近的一个最高点和最低点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$=( )| A. | $\frac{{π}^{2}}{4}$-1 | B. | $\frac{3{π}^{2}}{16}$-1 | C. | $\frac{3{π}^{2}}{4}$-1 | D. | $\frac{{π}^{2}}{8}$-1 |
分析 由题意可取α=0,则P(0,0),A($\frac{π}{4}$,1),B($\frac{3π}{4}$,-1),由向量的数量积可得.
解答 解:由题意可取α=0,则P(0,0),A($\frac{π}{4}$,1),B($\frac{3π}{4}$,-1),
∴$\overrightarrow{PA}$=($\frac{π}{4}$,1),$\overrightarrow{PB}$=($\frac{3π}{4}$,-1),
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=$\frac{π}{4}$×$\frac{3π}{4}$+1×(-1)=$\frac{3{π}^{2}}{16}$-1,
故选:B
点评 本题考查正弦函数图象,涉及平面向量数量积的运算和数形结合思想,属基础题.

练习册系列答案
相关题目
17.设p:?x∈R,x2-4x+3m>0,q:f(x)=x3+2x2+mx+1在(-∞,+∞)内单调递增,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.为了了解某天甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,
测量产品中的微量元素x,y的含量(单位:微克),当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.已知该天甲厂生产的产品共有98件,如表是乙厂的5件产品的测量数据:
(1)求乙厂该天生产的产品数量;
(2)用上述样本数据统计乙厂该天生产的优等品的数量;
(3)从乙厂抽取的上述5件产品中,随机抽取2件.求抽取的2件产品中优等品的件数X的分布列及数学期望.
测量产品中的微量元素x,y的含量(单位:微克),当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.已知该天甲厂生产的产品共有98件,如表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(2)用上述样本数据统计乙厂该天生产的优等品的数量;
(3)从乙厂抽取的上述5件产品中,随机抽取2件.求抽取的2件产品中优等品的件数X的分布列及数学期望.
11.2015年12月27日全国人大常委会表决通过了人口与计划生育法修正案全面二孩定于20I6年1月1日起正式实施,为了解适龄民众对放开生育二胎政策的态度,某机构从某市选取70后和80后作为调查对象.随机调查了100位,得到数据如下表:
(1)以这100个人的样本数据估计该市的总体数据,且以频率估计概率,若以该市70后公民中随机抽取3位,记其中生二孩的人数为X,求随机变量X的分布列和数学期望.
(2)根据调查数据,是否在犯错误的概率不超过0.1的前提下(有90%以上自把握)认为“生二孩与年龄有关”?并说明理由.
| 生二孩 | 不生二孩 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)根据调查数据,是否在犯错误的概率不超过0.1的前提下(有90%以上自把握)认为“生二孩与年龄有关”?并说明理由.
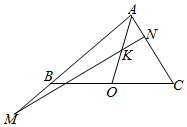 如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4.
如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4.