题目内容
2.已知椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{33}}{7}$,且(4,0)在椭圆C上,圆M:x2+y2=65.(1)求椭圆C的方程;
(2)已知A(m,n)为圆M上的任意一点,过点A作椭圆C的两条切线l1,l2,试探究直线l1,l2的位置关系,并说明理由.
分析 (1)由题意列关于a,b,c的方程组,求解方程组得到a,b的值,则椭圆方程可求;
(2)当过点A与椭圆C相切的一条切线的斜率不存在时,切线方程为x=±4,得到直线y=±7恰好为过点A与椭圆相切的另一条切线,于是两切线l1,l2互相垂直;当过点A(m,n)与椭圆C相切的切线的斜率存在时,设切线方程为y-n=k(x-m),联立直线方程和椭圆方程,得到关于x的一元二次方程,利用判别式等于0能推导出直线l1、l2始终相互垂直.
解答 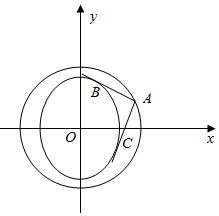 解:(1)由题意得$\left\{\begin{array}{l}{b=4}\\{\frac{c}{a}=\frac{\sqrt{33}}{7}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=7,b=4,
解:(1)由题意得$\left\{\begin{array}{l}{b=4}\\{\frac{c}{a}=\frac{\sqrt{33}}{7}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=7,b=4,
∴椭圆C的方程为$\frac{{y}^{2}}{49}+\frac{{x}^{2}}{16}=1$;
(2)如图,
①当过点A与椭圆C:$\frac{{y}^{2}}{49}+\frac{{x}^{2}}{16}=1$相切的一条切线的斜率不存在时,
此时切线方程为x=±4,
∵点A在圆M:x2+y2=65上,则A(±4,±7),
∴直线y=±7恰好为过点A与椭圆相切的另一条切线,于是两切线l1,l2互相垂直;
②当过点A(m,n)与椭圆C相切的切线的斜率存在时,
设切线方程为y-n=k(x-m),
由$\left\{\begin{array}{l}{y-n=k(x-m)}\\{\frac{{y}^{2}}{49}+\frac{{x}^{2}}{16}=1}\end{array}\right.$,
得(49+16k2)x2+32k(n-mk)x+16k2m2-32kmn+16n2-49×16=0,
由于直线与椭圆相切,
∴△=1024k2(n-mk)2-4(49+16k2)(16k2m2-32kmn+16n2-49×16)=0,
整理,得(16-m2)k2+2mnk+49-n2=0,
∴${k}_{1}{k}_{2}=\frac{49-{n}^{2}}{16-{m}^{2}}$,
∵P(m,n)在圆x2+y2=65上,∴m2+n2=65,
∴16-m2=n2-49,
∴k1k2=-1,则两直线互相垂直.
综上所述,直线l1、l2始终相互垂直.
点评 本题考查椭圆方程的求法,考查两直线的位置关系的判断,训练了两直线垂直与斜率的关系,体现了分类讨论的数学思想方法,注意函数与方程思想的合理运用,是中档题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案| A. | 直角三角形 | B. | 等腰三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| 生二孩 | 不生二孩 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
(2)根据调查数据,是否在犯错误的概率不超过0.1的前提下(有90%以上自把握)认为“生二孩与年龄有关”?并说明理由.
 已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0)为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点P在椭圆C上,且△PF1F2面积的最大值为$\sqrt{3}$.
已知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0)为椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,点P在椭圆C上,且△PF1F2面积的最大值为$\sqrt{3}$.