题目内容
8.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长是焦距的2倍,点(-1,-$\frac{3}{2}$)在椭圆C上,F1,F2分别是椭圆C的左、右焦点.(1)求椭圆C的方程;
(2)设P是椭圆C上的动点,直线PF1,PF2交椭圆C于A,B两点,$\overrightarrow{{F}_{1}A}$=λ$\overrightarrow{P{F}_{1}}$,$\overrightarrow{{F}_{2}B}$=μ$\overrightarrow{P{F}_{2}}$,求λ+μ的取值范围.
分析 (1)由题意知a=2c,b=$\sqrt{3}c$,从而可得$\frac{(-1)^{2}}{4{c}^{2}}$+$\frac{(-\frac{3}{2})^{2}}{3{c}^{2}}$=1,从而解得;
(2)设P(x,y),A(xA,yA),B(xB,yB),F1(-1,0),F2(1,0);从而可得$\left\{\begin{array}{l}{{x}_{A}=-λ-λx-1}\\{{y}_{A}=-λy}\end{array}\right.$,从而化简可得(2x+5)λ2+(2x+2)λ-3=0,从而解得λ=$\frac{3}{2x+5}$;同理u=$\frac{3}{-2x+5}$,从而解得.
解答  解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长是焦距的2倍,
解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长是焦距的2倍,
∴a=2c,b=$\sqrt{3}c$,
∴$\frac{(-1)^{2}}{4{c}^{2}}$+$\frac{(-\frac{3}{2})^{2}}{3{c}^{2}}$=1,
解得,c=1,a=2,b=$\sqrt{3}$,
故椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)设P(x,y),A(xA,yA),B(xB,yB),
F1(-1,0),F2(1,0);
∵$\overrightarrow{{F}_{1}A}$=λ$\overrightarrow{P{F}_{1}}$,
∴$\left\{\begin{array}{l}{{x}_{A}+1=-λ-λx}\\{{y}_{A}=-λy}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{A}=-λ-λx-1}\\{{y}_{A}=-λy}\end{array}\right.$,
又∵$\frac{{{x}_{A}}^{2}}{4}$+$\frac{{{y}_{A}}^{2}}{3}$=1,$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
∴(2x+5)λ2+(2x+2)λ-3=0,
∴λ=$\frac{3}{2x+5}$或λ=-1(舍去);
又∵$\overrightarrow{{F}_{2}B}$=μ$\overrightarrow{P{F}_{2}}$,
∴同理可得,
u=$\frac{3}{-2x+5}$,
∴λ+μ=$\frac{3}{2x+5}$+$\frac{3}{-2x+5}$
=$\frac{30}{25-4{x}^{2}}$∈($\frac{10}{13}$,$\frac{6}{5}$).
点评 本题考查了椭圆与直线的位置关系的应用及椭圆的标准方程的求法,同时考查了数形结合的思想应用.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{7}$ | D. | $\frac{2\sqrt{3}}{3}$ |
| A. | 0<a<1或a>2 | B. | 0<a<1或α≥2 | C. | 1<a≤2 | D. | 1≤a≤2 |
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
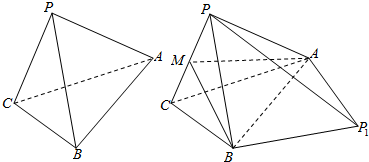 如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.
如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.