题目内容
14.已知双曲线与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1有相同的焦点,它的一条渐近线方程为y=x,求双曲线的方程.分析 由已知得双曲线的焦点坐标为F($±\sqrt{5}$,0),设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,(a>0,b>0),由双曲线的一条渐近线方程为y=x,能求出双曲线方程.
解答 解:∵双曲线与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1有相同的焦点,
∴双曲线的焦点坐标为F($±\sqrt{5}$,0),
∴设双曲线方程为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,(a>0,b>0),
∵双曲线的一条渐近线方程为y=x,
∴$\left\{\begin{array}{l}{a=b}\\{c=\sqrt{5}}\\{{c}^{2}={a}^{2}+{b}^{2}}\end{array}\right.$,解得a=b=$\sqrt{\frac{5}{2}}$,
∴双曲线方程为$\frac{{x}^{2}}{\frac{5}{2}}-\frac{{y}^{2}}{\frac{5}{2}}$=1.
点评 本题考查双曲线方程的求法,是中档题,解题时要认真审题,注意椭圆性质和双曲线性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知M=sin100°-cos100°,N=$\sqrt{2}$(cos46°•cos78°+cos44°•cos12°),P=$\frac{1-tan10°}{1+tan10°}$,Q=$\frac{tan22°+tan23°}{1-tan22°tan23°}$,那么M,N,P,Q之间的大小顺序是( )
| A. | M<N<P<Q | B. | P<Q<M<N | C. | N<M<Q<P | D. | Q<P<N<M |
4.已知向量$\overrightarrow{a}$=(λ,4λ-4),向量$\overrightarrow{b}$=(2,4),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则|$\overrightarrow{a}$|等于( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
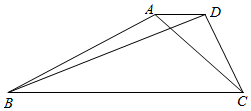 如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求:
如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2$\sqrt{10}$,∠CAD=$\frac{π}{4}$,tan∠ADC=-2,求: 如图在正方体ABCD-A1B1C1D1中,AC交BD于点O.
如图在正方体ABCD-A1B1C1D1中,AC交BD于点O.