题目内容
设cosx+cosy=
,sinx+siny=
,求cos(x-y)的值.
| 1 |
| 2 |
| 1 |
| 4 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:直接通过两个表达式平方,相加,即可通过两角差的余弦函数求解即可.
解答:
解:cosx+cosy=
,sinx+siny=
,
可得(sinx+siny)2=
,(cosx+cosy)2=
即sin2x+2sinxsiny+sin2y=
,cos2x+2cosxcosy+cos2y=
,
两式相加,可得:1+2(cosxcosy+sinxsiny)+1=
,
cosxcosy+sinxsiny=-
,
即cos(x-y)=-
.
| 1 |
| 2 |
| 1 |
| 4 |
可得(sinx+siny)2=
| 1 |
| 16 |
| 1 |
| 4 |
即sin2x+2sinxsiny+sin2y=
| 1 |
| 16 |
| 1 |
| 4 |
两式相加,可得:1+2(cosxcosy+sinxsiny)+1=
| 5 |
| 16 |
cosxcosy+sinxsiny=-
| 27 |
| 32 |
即cos(x-y)=-
| 27 |
| 32 |
点评:本题考查两角差的余弦函数以及同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
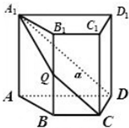 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则| B1Q |
| QB |
| A、1 | ||
| B、2 | ||
| C、3 | ||
D、与
|
 如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )
如图所示,现有一迷失方向的小青蛙在3处,它每跳动一次可以等可能地进入相邻的任意一格(若它在5处,跳动一次,只能进入3处,若在3处,则跳动一次可以等机会进入1,2,4,5处),则它在第三次跳动后,首次进入5处的概率是( )