题目内容
已知a∈R,b>0,则(a-b)2+(a+2+b2-3lnb)2的最小值为 .
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:令
,
,分别化为y=x+2,y=3lnx-x2.因此求出(a-b)2+(a+2+b2-3lnb)2的最小值等价于求出直线y=x+2与曲线y=3lnx-x2之间的距离的平方的最小值.利用导数的几何意义及其点到直线的距离公式即可得出.
|
|
解答:
解:令
,
,
分别化为y=x+2,y=3lnx-x2.
因此求出(a-b)2+(a+2+b2-3lnb)2的最小值等价于求出直线y=x+2与曲线y=3lnx-x2之间的距离的平方的最小值.
设与直线y=x+2平行且与曲线y=3lnx-x2相切于点P(x0,y0).
则y′=
-2x|x=x0=1,解得x0=1,
∴切点P(1,-1).
点P到直线y=x+2的距离d=
=2
,
∴(a-b)2+(a+2+b2-3lnb)2的最小值为(2
)2=8.
故答案为:8.
|
|
分别化为y=x+2,y=3lnx-x2.
因此求出(a-b)2+(a+2+b2-3lnb)2的最小值等价于求出直线y=x+2与曲线y=3lnx-x2之间的距离的平方的最小值.
设与直线y=x+2平行且与曲线y=3lnx-x2相切于点P(x0,y0).
则y′=
| 3 |
| x |
∴切点P(1,-1).
点P到直线y=x+2的距离d=
| |1+1+2| | ||
|
| 2 |
∴(a-b)2+(a+2+b2-3lnb)2的最小值为(2
| 2 |
故答案为:8.
点评:本题考查了导数的几何意义、切线方程、点到直线的距离公式,考查了问题等价转化方法,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
直线
x+y-b=0截圆x2+y2-4y=0所得的劣弧所对的圆心角为
,则实数b的值是( )
| 3 |
| 2π |
| 3 |
A、2+2
| ||
| B、4 | ||
C、2±2
| ||
| D、0或4 |
 幼儿园的一个小朋友正在给一个圆、一个三角形和一个长方形着色,有红,蓝两种颜色可供选择,对于每一个图形,他都随机地选择一种颜色涂上.
幼儿园的一个小朋友正在给一个圆、一个三角形和一个长方形着色,有红,蓝两种颜色可供选择,对于每一个图形,他都随机地选择一种颜色涂上.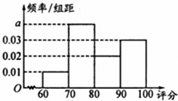 为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.
为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.