题目内容

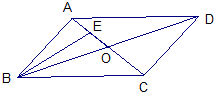如图，在平面四边形ABCD中，AC，BD相交于点O，E为线段AO的中点，若
BE
=λ
BA
+μ
BD
（λ，μ∈R），则 λ+μ=
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：
BD
=2
BO
，
BE
=λ
BA
+μ
BD
，可得
BE
=λ
BA
+2μ
BO
．由E为线段AO的中点，可得
BE
=
1
2
(
BA
+
BO
)，再利用平面向量基本定理即可得出．
解答： 解：∵
BD
=2
BO
，
BE
=λ
BA
+μ
BD
，
∴
BE
=λ
BA
+2μ
BO
，
∵E为线段AO的中点，
∴
BE
=
1
2
(
BA
+
BO
)，
∴λ=
1
2
，2μ=
1
2
，
解得μ=
1
4
，
∴λ+μ=
3
4
．
故答案为：
3
4
．
点评：本题考查了平面向量基本定理、向量共线定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
在△ABC中，A，B的坐标分别是(-
2
，0)，(
2
，0)，点G是△ABC的重心，y轴上一点M满足GM∥AB，且|MC|=|MB|．
（Ⅰ）求△ABC的顶点C的轨迹E的方程；
（Ⅱ）直线l：y=kx+m与轨迹E相交于P，Q两点，若在轨迹E上存在点R，使四边形OPRQ为平行四边形（其中O为坐标原点），求m的取值范围．
四面体ABCD的体积是
1
6
，△ABC是斜边AB=2的等腰直角三角形，若点A，B，C，D都在半径为
2
的同一球面上，则D与AB中点的距离是
 
．
若双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的渐近线与圆（x-2）2+y2=1相切，则双曲线的离心率为（　　）
A、2
B、
3
2
C、
2
3
3
D、
3
为检测某种零件的生产质量，检验人员抽取了同批次的零件作为样本进行检测并评分，若检测后评分结果大于60分的零件为合格零件．
（1）已知200个合格零件评分结果的频率分布直方图如图所示，请根据此频率分布直方图，估计这200个零件评分结果的平均数和中位数；
（2）现有7个零件的评分结果为（单位：分）：63，73，75，76，78，85，91，若从评分结果在（60，80]内的所有零件中随机抽取3个，求恰有2个零件的评分结果在（70，80]内的概率．
如图，一架飞机从A地飞到B地，两地相距700km．飞行员为了避开某一区域的雷雨云层，从机场起飞后，就沿与原来飞行方向成21°角的方向飞行，飞行到中途，再沿与原来的飞行方向成35°夹角的方向继续飞行直到终点．这样飞机的飞行路程比原来路程700km远了多少？
下列三个命题：
①若
A1A2
+
A2A3
+
A3A1
=
0
，则A1，A2，A3三点共面；
②若
A1A2
+
A2A3
+
A3A4
+
A4A1
=
0
，则A1，A2，A3，A4四点共面；
③若
A1A2
+
A2A3
+
A3A4
+…+
An-1An
+
AnA1
=
0
，则A1，A2，A3，…，An这n个点共面．
其中是真命题的为（　　）
A、①B、②C、①②D、①②③
在△ABC中，内角A，B，C的对边分别是a，b，c，已知
2cosC-cosA
cosB
=
a-2c
b
．
（1）求
c
a
的值；
（2）若cosB=
2
3
，△ABC面积为
5
6
，求b的值．
若
1+2i
x+yi
为实数（x，y∈R，那么x，y满足的关系式为（　　）
A、y=2xB、y=-2x
C、x=2yD、x=-2y

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网