题目内容
18．${（{\sqrt{2}x-\frac{1}{x^2}}）^3}$的展开式中常数项为（ ）| A． | -6 | B． | -2 | C． | 2 | D． | 6 |
分析 根据二项式展开式的通项公式，令x的指数为0求出r的值，即可求出展开式中常数项．
解答 解：${（{\sqrt{2}x-\frac{1}{x^2}}）^3}$的展开式的通项公式为
Tr+1=${C}_{3}^{r}$•${（\sqrt{2}x）}^{3-r}$•${（-\frac{1}{{x}^{2}}）}^{r}$
=（-1）r•${（\sqrt{2}）}^{3-r}$•${C}_{3}^{r}$•x3-3r，
令3-3r=0，解得r=1，
∴${（{\sqrt{2}x-\frac{1}{x^2}}）^3}$展开式中常数项为
T2=-1×${（\sqrt{2}）}^{2}$×${C}_{3}^{1}$=-6．
故选：A．
点评 本题考查了二项式展开式中的通项公式应用问题，是基础题目．
练习册系列答案
快捷英语周周练系列答案
相关题目
3．已知集合A={x|-1＜x＜5}，B={x|x2≥4}，则∁R（A∪B）=（ ）
| A． | （-2，-1） | B． | （2，5） | C． | （-2，-1] | D． | （-∞，2）∪[5，+∞） |
16．
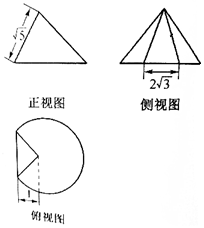一个圆锥被过顶点的平面截去了较少的一部分几何体，余下的几何体的三视图如图，则余下部分的几何体的体积为（ ）
一个圆锥被过顶点的平面截去了较少的一部分几何体，余下的几何体的三视图如图，则余下部分的几何体的体积为（ ）| A． | $\frac{8π}{3}$+$\sqrt{15}$ | B． | $\frac{16π}{3}$+$\sqrt{3}$ | C． | $\frac{8π}{3}$+$\frac{2\sqrt{3}}{3}$ | D． | $\frac{16π}{9}$+$\frac{2\sqrt{3}}{3}$ |
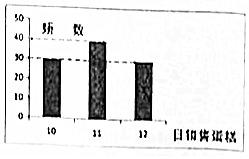某超市每两天购入一批某型号的生日蛋糕进行销售，进价50元/个，售价60元/个，若每次购入的生日蛋糕两天内没有售完，则以40元/个的价格可以全部处理掉，根据此超市以往随机抽取的100天此类蛋糕的销售情况，如柱形图所示．设n为每次购入的蛋糕数，ξ为两天内的蛋糕销售数量，W为此批购入的蛋糕销售的利润（视频率为概率，且每天销售情况是独立的）