题目内容
1.设函数f(x)=$\left\{\begin{array}{l}{{e}^{x-1},x<1}\\{lo{g}_{2}x,x≥1}\end{array}\right.$,则使得f(x)≤1成立的x的取值范围是(-∞,2].分析 根据分段函数的表达式,对x进行分类讨论进行求解即可.
解答 解:若x≥1,由f(x)≤1得1得log2x)≤1,即0<x≤2,即1≤x≤2,
若x<1,则由f(x)≤1得ex-1≤1,即x-1≤0,得x≤1,此时x<1,
综上x≤2,
即不等式的解集为(-∞,2],
故答案为:(-∞,2]
点评 本题主要考查不等式的求解,根据分段函数的表达式,对x进行分类讨论是解决本题的关键.

练习册系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}ln(x+1),x>0\\ \frac{1}{2}x+1,x≤0\end{array}\right.$,若m<n,且f(m)=f(n),则n-m的取值范围是( )
| A. | [3-2ln2,2) | B. | [3-2ln2,2] | C. | [e-1,2] | D. | [e-1,2) |
13.${∫}_{-2}^{-1}$$\frac{2}{x}$dx=( )
| A. | -ln2 | B. | ln2 | C. | -2ln2 | D. | 2ln2 |
10.已知sin($\frac{π}{5}-α$)=$\frac{1}{3}$,则cos(2$α+\frac{3π}{5}$)=( )
| A. | -$\frac{7}{9}$ | B. | -$\frac{1}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{7}{9}$ |
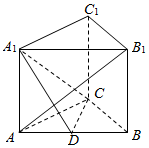 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.