题目内容
已知数列{an}的前n项和为Sn,且满足Sn=2an-4(n∈N*),则an= ;数列{log2an}的前n项和为 .
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出{an}是首项为4,公比为2的等比数列,所以an=4×2n-1=2n+1.log2an=n+1,由此能求出数列{log2an}的前n项和.
解答:
解:∵Sn=2an-4(n∈N*),
∴n=1时,a1=S1=2a1-4,解得a1=4,
n≥2时,an=Sn-Sn-1=2an-2an-1,
整理,得an=2an-1,
∴{an}是首项为4,公比为2的等比数列,
∴an=4×2n-1=2n+1.
log2an=n+1,
∴数列{log2an}的前n项和为:
2+3+4+5+…+(n+1)=
.
故答案为:2n+1,
.
∴n=1时,a1=S1=2a1-4,解得a1=4,
n≥2时,an=Sn-Sn-1=2an-2an-1,
整理,得an=2an-1,
∴{an}是首项为4,公比为2的等比数列,
∴an=4×2n-1=2n+1.
log2an=n+1,
∴数列{log2an}的前n项和为:
2+3+4+5+…+(n+1)=
| n(n+3) |
| 2 |
故答案为:2n+1,
| n(n+3) |
| 2 |
点评:本题考查数列的通项公式和前n项和公式的求法,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
在-2π~0内与
π终边相同的角是( )
| 52 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
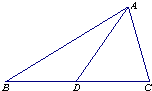 如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=
如图,在△ABC中,点D在BC边上,AD=33,sin∠BAD=