题目内容
如果椭圆
+
=1上一点P到焦点F1的距离为6，则点P到另一个焦点F2的距离为（ ）
| x2 |
| 100 |
| y2 |
| 36 |
| A、10 | B、6 | C、12 | D、14 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据椭圆的定义|PF1|+|PF2|=2a，利用|PF1|=6，可求|PF2|
解答：
解：由椭圆的定义知|PF1|+|PF2|=2a=20，
∵|PF1|=6，∴|PF2|=14．
故选：D．
∵|PF1|=6，∴|PF2|=14．
故选：D．
点评：本题给出椭圆上一点到一个焦点的距离，求它到另一个焦点的距离．着重考查了椭圆的定义、标准方程与简单几何性质等知识，属于基础题．
练习册系列答案
相关题目
曲线y=x3-2x+2014在点（1，2013）处的切线的倾斜角为（ ）
| A、30° | B、60° |
| C、45° | D、120° |
某班有4个空位，安排从外校转来的3个学生坐到这4个空位上，每人一个座位，则不同的坐法有（ ）
| A、24种 |
| B、43种 |
| C、34种 |
| D、4种 |
已知集合M={1，2，3}，N={2，3，4}，则M∩N=（ ）
| A、{2，3} |
| B、{1，2，3，4} |
| C、{1，4} |
| D、∅ |
当x=5时．用秦九韶算法计算f（x）=12x6+5x5+11x2+2x+5的值时，需要进行的乘法和加法的次数分别是（ ）
| A、12，6 | B、6，6 |
| C、15，4 | D、6，4 |
定义
为n个正数x1，x2，…，xn的“平均倒数”．若正项数列{an}的前n项的“平均倒数”为
，则数列{an}的通项公式为an=（ ）
| n |
| x1+x2+…xn |
| 1 |
| 3n+2 |
| A、3n+2 |
| B、6n-1 |
| C、（3n-1）（3n+2） |
| D、4n+1 |
曲线y=x2+2与直线5x-y+2=0所围成的图形面积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
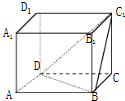如图长方体ABCD-A1B1C1D1中，AB=AD=2