Question

6．已知函数y=（x+1）^-2+2．
（1）作出函数y的图象；
（2）确定随x的增加，函数值y的变化情况；
（3）比较f（-2）与f（-$\frac{\sqrt{2}}{2}$）的大小．

Answer 1

分析 （1）函数y=x^-2是偶函数，在（0，+∞）上递减，以坐标轴为渐近线，且过点（1，1）．
（2）利用函数图象可得出函数单调区间；
（3）由函数图象关于x=-1对称，可得f（-2）=f（0）；利用单调性可得f（-$\frac{\sqrt{2}}{2}$）＞f（0），进而得出答案．

解答 解：（1）先做出偶函数y=x^-2的图象，
再向左平移1个单位，
最后向上平移2个单位．得到y=（x+1）^-2+2的图象；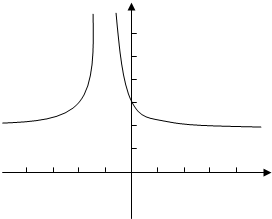

（2）由图象可知：
当x∈（-∞，-1）时，随x的增加，函数值y也增加；
当x∈（-1，+∞）时，随x的增加，函数值y减小；
（3）由图可知f（-2）=f（0）；
f（-$\frac{\sqrt{2}}{2}$）＞f（0），
∴f（-$\frac{\sqrt{2}}{2}$）＞f（-2）．

点评 考察了图象的平移变换和利用图象解决实际问题．