题目内容

16．已知C${\;}_{n+1}^{7}$-C${\;}_{n}^{7}$=C${\;}_{n}^{8}$（n∈N*），则n等于（　　）
A．14B．12C．13D．15

分析 由已知条件结合组合数公式的性质得到${C}_{n+1}^{7}={C}_{n}^{8}+{C}_{n}^{7}={C}_{n+1}^{8}$，由此能求出n．

解答 解：∵C${\;}_{n+1}^{7}$-C${\;}_{n}^{7}$=C${\;}_{n}^{8}$（n∈N*），
∴${C}_{n+1}^{7}={C}_{n}^{8}+{C}_{n}^{7}={C}_{n+1}^{8}$，
∴n+1=7+8，解得n=14．
故选：A．

点评 本题考查自然数n的求法，是基础题，解题时要认真审题，注意组合数公式的合理运用．

练习册系列答案
相关题目
6．计算求值
①求值：cos2π-sin$\frac{3π}{2}+cosπ-sin\frac{π}{2}$；
②当α=-$\frac{π}{6}$时，求$\frac{sin（2π-α）•cos（π+α）}{cos（π-α）sin（3π-α）sin（-α-π）}$值．
7．若等比数列{an}的前项和为Sn，且$\frac{{s}_{10}}{{s}_{20}}$=$\frac{2}{3}$，则$\frac{{s}_{20}}{{s}_{40}}$=（　　）
A．$\frac{2}{5}$B．$\frac{4}{5}$C．$\frac{4}{7}$D．$\frac{3}{4}$
4．（Ⅰ）已知tanθ=-$\frac{3}{4}$，求2+sinθ．cosθ-cos2θ的值；
（Ⅱ）已知sin（α-3π）=2cos（α-4π），求$\frac{{sin（{π-α}）+5cos（{2π-α}）}}{{2sin（{\frac{3π}{2}-α}）-sin（{-α}）}}$的值．
11．如图，函数的图象在P点处的切线方程是y=-x+8，若点P的横坐标是5，则f（5）+f′（5）=（　　）
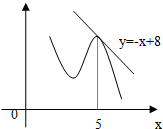
A．$\frac{1}{2}$B．1C．2D．0
1．已知f1（x）=x，且对任意的n∈N*，fn（1）=1，f′n+1（x）=fnx+xf′nx．
（1）求fn（x）的解析式；
（2）设函数gn（x）=fn（x）+fn（m-x），x∈（0，m），m＞0，对于任意的三个数${x_1}，{x_2}，{x_3}∈[\frac{m}{2}，\frac{2m}{3}]$，以g3（x1），g3（x2），g3（x3）的值为边长的线段是否可构成三角形？请说明理由．
8．设集合A={x|x2-3x+2=0}，B={x|（x-1）（x-a+1）=0}，C={x|x2-mx+2=0}，若A∪B=A，A∩C=C．
（Ⅰ）求实数a的取值集合；
（Ⅱ）求实数m的取值集合．
5．函数$f（x）=tan（3x-\frac{π}{4}）$的定义域为{x|x≠$\frac{kπ}{3}$+$\frac{π}{4}$，k∈Z}．
6．已知函数y=（x+1）-2+2．
（1）作出函数y的图象；
（2）确定随x的增加，函数值y的变化情况；
（3）比较f（-2）与f（-$\frac{\sqrt{2}}{2}$）的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网