题目内容
1.求证:函数$f(x)=\frac{1}{x}+1$在(0,+∞)上是减函数.分析 利用定义证明函数f(x)在(0,+∞)是减函数,基本步骤是取值、作差、判正负和下结论.
解答 证明:任取x1,x2∈(0,+∞),且x1<x2;
则f(x1)-f(x2)=$\frac{{{x_2}-{x_1}}}{{{x_1}{x_2}}}$,
∵x1,x2∈(0,+∞),且x1<x2,
∴f(x1)-f(x2)>0,
即f(x1)>f(x2);
∴函数f(x)在(0,+∞)是减函数.
点评 本题考查了利用定义来证明函数的单调性问题,是基础题目.

练习册系列答案
相关题目
11.如图,函数的图象在P点处的切线方程是y=-x+8,若点P的横坐标是5,则f(5)+f′(5)=( )
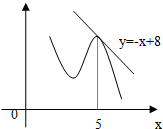

| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 0 |
12.函数f(x)=lg(lgx)的定义域为( )
| A. | (0,+∞) | B. | (0,1) | C. | (0,1] | D. | (1,+∞) |



