题目内容
复数
在复平面上对应的点位于（ ）
| 1-2i |
| 3+4i |
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
考点：复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：利用复数的运算法则和几何意义即可得出．
解答：
解：复数
=
=
=-
-
i对应的点(-
，-
)在第三象限，
故选：B．
| 1-2i |
| 3+4i |
| (1-2i)(3-4i) |
| (3+4i)(3-4i) |
| -5-10i |
| 25 |
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
故选：B．
点评：本题考查了复数的运算法则和几何意义，属于基础题．
练习册系列答案
相关题目
如果复数z满足条件z+|z|=3+i，那么z等于（ ）
A、
| ||
B、-
| ||
C、-
| ||
D、
|
已知数列{an}，an+1=kan+3（k＞0），其中a1=0，a4=9，则k等于（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
实数对（x，y）满足不等式组
，若目标函数z=2kx-y在x=3，y=1时取最大值，则k的取值范围是（ ）
|
A、（-∞，-
| ||||
B、[-
| ||||
C、[-
| ||||
D、（-∞，-
|
复数z=
的共轭复数是（ ）
| i |
| 1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知sin（π+α）=
，则cos（
-α）=（ ）
| 1 |
| 3 |
| 3π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
在△ABC中，角A，B，C所对的边分别为5，7，8，则∠B的大小是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
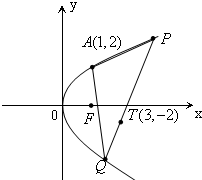点A（1，2）到抛物线y2=2px（p＞0）的焦点F的距离为2，过T（3，-2）的动直线l与此抛物线交于P、Q两点