题目内容
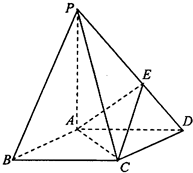 如图,在底面为棱形的四棱锥P-ABCD在那个,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为棱形的四棱锥P-ABCD在那个,∠ABC=60°,PA=AC=1,PB=PD=| 2 |
(1)求证:PA⊥平面ABCD;
(2)求二面角E-AC-D的正弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)直接利用勾股定理的逆定理求得线线垂直,进一步利用线面垂直的判定定理,求得结论.
(2)先做出二面角的平面角,再利用相关的比例问题求得线段长,最后求得结果.
(2)先做出二面角的平面角,再利用相关的比例问题求得线段长,最后求得结果.
解答:
(1)证明:四棱锥P-ABCD的底面为菱形,∠ABC=60°AC=1,
所以△ABC为等边三角形.
解得AB=BC=1
PA=1,PB=PD=
所以:PA2+AB2=PB2,PA2+AD2=PD2
所以:PA⊥AB,PA⊥AD
即:PA⊥平面ABCD
(2)解:连接AC,BD交与点0,过点E做EF⊥AD于F,在平面ABCD中做FH⊥AC
连接EH,所以∠EHF即为二面角E-AC-D的平面角.
所以利用:PE:ED=2:1.
=
解得:EF=
同理解得:FH=
则:在直角三角形EFH中,tan∠EHF=
所以:∠EHF=
即:sin∠EHF=

所以△ABC为等边三角形.
解得AB=BC=1
PA=1,PB=PD=
| 2 |
所以:PA2+AB2=PB2,PA2+AD2=PD2
所以:PA⊥AB,PA⊥AD
即:PA⊥平面ABCD
(2)解:连接AC,BD交与点0,过点E做EF⊥AD于F,在平面ABCD中做FH⊥AC
连接EH,所以∠EHF即为二面角E-AC-D的平面角.
所以利用:PE:ED=2:1.
| EF |
| AP |
| 1 |
| 3 |
| 1 |
| 3 |
同理解得:FH=
| ||
| 3 |
则:在直角三角形EFH中,tan∠EHF=
| ||
| 3 |
所以:∠EHF=
| π |
| 6 |
即:sin∠EHF=
| 1 |
| 2 |

点评:本题考查的知识要点:线面垂直的判定定理,勾股定理逆定理的应用,平面角二面角的做法,相关的比例问题,属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当x=2时,如图的程序结果是( )


| A、3 | B、7 | C、15 | D、17 |
设集合M={-1,0,1},N={x|x2≤x},M∩N=( )
| A、{0} |
| B、{0,1} |
| C、{-1,1} |
| D、{-1,0} |
已知集合A={1,3,5,7,9},B={0,3,6,9,12},则A∩(∁NB)=( )
| A、{1,2,3} |
| B、{1,3,9} |
| C、{1,5,7} |
| D、{3,5,7} |
已知点P是抛物线y2=4x上的动点,点P在y轴上的射影是M,点A 的坐标是(4,a),则当|a|>4时,|PA|+|PM|的最小值是( )
A、
| ||
B、
| ||
| C、a+3 | ||
D、
|
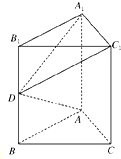 如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.
如图所示,在直三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1中点,求证:AD⊥平面A1DC1.