题目内容
7.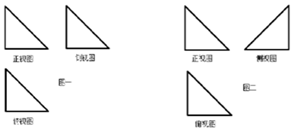 小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )
小明在解决三视图还原问题时,错把图一的三视图看成图二的三视图,假设图一所对应几何体中最大的面积为S1,图二所对应几何体中最大面的面积为S2,三视图中所有三角形均为全等的等腰直角三角形,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | 1 | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 根据已知中的三视图,分别求出两个几何体中面积最大的面,进而可得答案
解答 解:假设三视图中全等的等腰直角三角形的腰长为a,
则图一的三视图对应的几何体中,
面积最大的面是直角边长为:a,$\sqrt{2}a$的直角三角形,
故S1=$\frac{\sqrt{2}}{2}{a}^{2}$,
图二的三视图对应的几何体中,
面积最大的面是边长为:$\sqrt{2}a$的等边三角形,故S2=$\frac{\sqrt{3}}{4}•(\sqrt{2}a)^{2}$=$\frac{\sqrt{3}}{2}{a}^{2}$,
故$\frac{{S}_{1}}{{S}_{2}}$=$\frac{\frac{\sqrt{2}}{2}{a}^{2}}{\frac{\sqrt{3}}{2}{a}^{2}}$=$\frac{\sqrt{6}}{3}$,
故选:D
点评 本题考查的知识点是空间几何体的三视图,三角形面积公式,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设集合A={x∈Z|x2-2x-3≤0},B={0,1},则∁AB=( )
| A. | {-3,-2,-1} | B. | {-1,2,3} | C. | {-1,0,1,2,3} | D. | {0,1} |
2.若0<x1<x2<1,则( )
| A. | ex2-ex1>lnx2-lnx1 | B. | ex2-ex1<lnx2-lnx1 | ||
| C. | x2ex1>x1ex2 | D. | x2ex1<x1ex2 |
12.当x>0时,函数f(x)=(aex+b)(x-2)单调递增,且函数y=f(x-1)的图象关于直线x=1对称,则使得f(2-m)>0成立的m的取值范围是( )
| A. | {m|m<-2或m>2} | B. | {m|-2<m<2} | C. | {m|m<0或m>4} | D. | {m|0<m<4} |
17.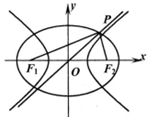 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )| A. | e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | B. | e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | ||
| C. | e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ | D. | e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ |
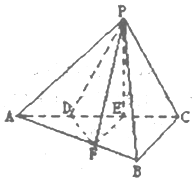 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,∠ABC=$\frac{π}{2}$,点D、E在线段AC上,且AD=DE=EC=1,PD=PC=2,点F在线段AB上,且EF∥BC.