题目内容
7.某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.(1)求该乐队至少演唱1首原创新曲的概率;
(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a,求观众与乐队的互动指数之和X的概率分布及数学期望.
分析 (1)设“该乐队至少演唱1首原创新曲”的事件为A,则P(A)=1-P$(\overline{A})$.
(2)由题意可得:X=5a,6a,7a,8a.利用“超几何分布列”即可得出.
解答 解:(1)设“该乐队至少演唱1首原创新曲”的事件为A,则P(A)=1-P$(\overline{A})$=1-$\frac{{∁}_{5}^{4}}{{∁}_{8}^{4}}$=$\frac{13}{14}$.
(2)由题意可得:X=5a,6a,7a,8a.
P(X=5a)=$\frac{{∁}_{3}^{3}{∁}_{5}^{1}}{{∁}_{8}^{4}}$=$\frac{5}{70}$=$\frac{1}{14}$,P(X=6a)=$\frac{{∁}_{3}^{2}{∁}_{5}^{2}}{{∁}_{8}^{4}}$=$\frac{30}{70}$=$\frac{3}{7}$,
P(X=7a)=$\frac{{∁}_{3}^{1}{∁}_{5}^{3}}{{∁}_{8}^{4}}$=$\frac{30}{70}$=$\frac{3}{7}$,P(X=8a)=$\frac{{∁}_{5}^{4}}{{∁}_{8}^{4}}$=$\frac{5}{70}$=$\frac{1}{14}$.
| X | 5a | 6a | 7a | 8a |
| P | $\frac{1}{14}$ | $\frac{3}{7}$ | $\frac{3}{7}$ | $\frac{1}{14}$ |
点评 本题考查了“超几何分布列”的概率计算公式数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.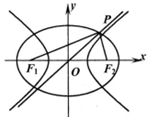 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
 如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )
如图,点F1、F2是椭圆C1、C2的左右焦点,椭圆C1与双曲线C2的渐近线交于点P,PF1⊥PF2,椭圆C1与双曲线C2的离心率分别为e1、e2,则( )| A. | e22=$\frac{1+{{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | B. | e22=$\frac{{2{e}_{1}}^{4}}{1-{{e}_{1}}^{2}}$ | ||
| C. | e22=$\frac{1-{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ | D. | e22=$\frac{{{e}_{1}}^{4}}{2{{e}_{1}}^{2}-1}$ |
18.《九章算术》有这样一个问题:今有女子善织,日增等尺,第二日、第五日、第八日所织之和为十五尺,九日共织尺数是( )
| A. | 5 | B. | 15 | C. | 45 | D. | 10 |
12.已知a=20.1,$b={({\frac{1}{2}})^{-0.4}}$,c=2log72,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | b<c<a |
20.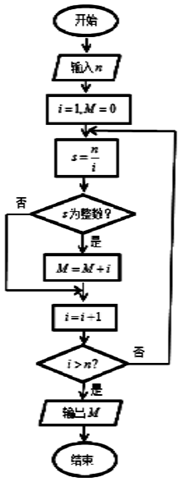 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )| A. | 66 | B. | 65 | C. | 64 | D. | 63 |
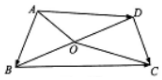 如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.
如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.