已知经过点P(2.0).斜率为$\frac{4}{3}$的直线和抛物线y2=2x相交于A.B两点.设线段AB中点为M.求点M的坐标．题目和参考答案——青夏教育精英家教网—

题目内容

16．已知经过点P（2，0），斜率为$\frac{4}{3}$的直线和抛物线y²=2x相交于A，B两点，设线段AB中点为M，求点M的坐标．

分析由题意可得直线l得方程为y=$\frac{4}{3}$（x-2），联立y=$\frac{4}{3}$（x-2）与y²=2x，得8x²-41x+32=0，结合方程的根与系数的关系及中点坐标公式可求M点的坐标．

解答解：由题意可得直线l得方程为y=$\frac{4}{3}$（x-2）
联立y=$\frac{4}{3}$（x-2）与y²=2x，得8x²-41x+32=0
设A（x₁，y₁）B（x₂，y₂）则x₁+x₂=$\frac{41}{8}$，y₁+y₂=$\frac{3}{2}$
∵线段AB中点为M，
∴M点的坐标（$\frac{41}{16}$，$\frac{3}{4}$）．

点评本题主要考查了直线与抛物线的相交关系的应用，方程思想及方程的根与系数的关系的应用是解决本题的关键．

练习册系列答案

相关题目

6．已知x²-5ax+25＞0，对x∈R恒成立，求实数a的取值范围．

7．化简：
（1）（sinα+cosα）²+（sinα-cosα）²；
（2）sin²α（1+$\frac{1}{tan^2α}$）

4．已知方程y=kx+13和x²+y²=144，当k为何值时，它们的曲线只有一个交点？

11．当-$\frac{π}{2}$≤x≤$\frac{π}{2}$时，函数f（x）=2sin（x+$\frac{π}{3}$）有（　　）

	A．	最大值1，最小值-1		B．	最大值1，最小值-$\frac{1}{2}$
	C．	最大值2，最小值-2		D．	最大值2，最小值-1

3．

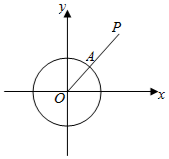在平面直角坐标系xOy中，对于⊙O：x²+y²=1来说，P是坐标系内任意一点，点P到⊙O的距离S_P的定义如下：若P与O重合，S_P=r；若P不与O重合，射线OP与⊙O的交点为A，S_P=AP的长度（如图）．
（1）直线2x+2y+1=0在圆内部分的点到⊙O的最长距离为1-$\frac{\sqrt{2}}{4}$；
（2）若线段MN上存在点T，使得：
①点T在⊙O内；
②?点P∈线段MN，都有S_T≥S_P成立．则线段MN的最大长度为4．

10．在直角坐标系xOy中，曲线C的参数方程为$\left\{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}\right.$（α为参数），在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为ρsin（$θ+\frac{π}{4}$）=2$\sqrt{2}$．
（Ⅰ）分别将曲线C的参数方程和直线l的极坐标方程转化为直角坐标系下的普通方程；
（Ⅱ）动点A在曲线C上，动点B在直线l上，定点P的坐标为（-2，2），求|PB|+|AB|的最小值．

7．已知命题p：?x∈（0，$\frac{π}{2}$），使得cosx≥x，则该命题的否定是（　　）

	A．	?x∈（0，$\frac{π}{2}$），使得cosx＞x		B．	?x∈（0，$\frac{π}{2}$），使得cosx≥x
	C．	?x∈（0，$\frac{π}{2}$），使得cosx＜x		D．	?x∈（0，$\frac{π}{2}$），使得cosx＜x

试题分类