题目内容
设函数f(x)=sin(2x+
)+cos2x+
sinxcosx.
(1)已知x∈[0,
],求函数f(x)的值域;
(2)设A,B,C为△ABC的三个内角,若cosB=
,f(
)=
,求sinA.
| π |
| 6 |
| 3 |
(1)已知x∈[0,
| π |
| 2 |
(2)设A,B,C为△ABC的三个内角,若cosB=
| 1 |
| 3 |
| C |
| 2 |
| 5 |
| 2 |
考点:三角函数中的恒等变换应用,两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:(1)化简f(x)=2sin(2x+
)+
,由于x∈[0,
],2x+
∈[
,
],所以函数f(x)的最大值是
,函数f(x)的最小值是-
,即可求出值域.
(2)f(
)=2sin(C+
)+
=
,所以sin(C+
)=1,又C为△ABC的内角 所以C=
,又因为在△ABC中,cosB=
,所以sinB=
,所以sinA的值为
.
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| 5 |
| 2 |
| 1 |
| 2 |
(2)f(
| c |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 5 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
2
| ||||
| 6 |
解答:
解:(1)f(x)=
sin2x+
cos2x+
+
sin2x
=
sin2x+cos2x+
=2sin(2x+
)+
x∈[0,
],2x+
∈[
,
],
所以函数f(x)的最大值是
,函数f(x)的最小值是-
,
故函数f(x)的值域为[-
,
].
(2)f(
)=2sin(C+
)+
=
,所以sin(C+
)=1,
又C为△ABC的内角 所以C=
,
又因为在△ABC 中,cosB=
,所以sinB=
,所以
sinA=sin(B+C)=sinBcosC+cosBsinC=
×
+
×
=
.
| ||
| 2 |
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| ||
| 2 |
=
| 3 |
| 1 |
| 2 |
=2sin(2x+
| π |
| 6 |
| 1 |
| 2 |
x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
所以函数f(x)的最大值是
| 5 |
| 2 |
| 1 |
| 2 |
故函数f(x)的值域为[-
| 1 |
| 2 |
| 5 |
| 2 |
(2)f(
| c |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| 5 |
| 2 |
| π |
| 6 |
又C为△ABC的内角 所以C=
| π |
| 3 |
又因为在△ABC 中,cosB=
| 1 |
| 3 |
2
| ||
| 3 |
sinA=sin(B+C)=sinBcosC+cosBsinC=
2
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
2
| ||||
| 6 |
点评:本题主要考察了三角函数中的恒等变换应用,两角和与差的余弦函数,学生的计算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=3sin(2x-
)的图象为M,下列结论中正确的是( )
| π |
| 3 |
A、图象M关于直线x=
| ||||
B、图象M关于点(-
| ||||
C、f(x)在区间(-
| ||||
D、由y=3sin2x的图象向右平移
|
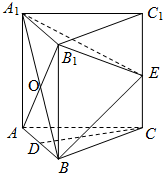 如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,E为侧棱CC1的中点.