题目内容
集合A={x|x2+6x=0},B={x2+3(a+1)x+a2-1=0},全集为R,且A∪B=A,求实数a的取值范围.
考点:并集及其运算
专题:计算题,集合
分析:由题意化简A={x|x2+6x=0}={0,-6},从而可得B=∅,或{0}或{-6}或{0,-6};分类讨论解出即可.
解答:
解:A={x|x2+6x=0}={0,-6},
∵A∪B=A,
∴B⊆A;
故B=∅,或{0}或{-6}或{0,-6};
若B=∅,则△=(3(a+1))2-4(a2-1)<0,
解得,-
<a<-1;
当B={0},则a2-1=0,3(a+1)=0;
解得,a=-1;
当B={-6},则a2-1=36,3(a+1)=12;
无解;
当B={0,-6},则a2-1=0,3(a+1)=6;
解得,a=1;
故实数a的取值范围为{a|-
<a≤-1或a=1}.
∵A∪B=A,
∴B⊆A;
故B=∅,或{0}或{-6}或{0,-6};
若B=∅,则△=(3(a+1))2-4(a2-1)<0,
解得,-
| 13 |
| 5 |
当B={0},则a2-1=0,3(a+1)=0;
解得,a=-1;
当B={-6},则a2-1=36,3(a+1)=12;
无解;
当B={0,-6},则a2-1=0,3(a+1)=6;
解得,a=1;
故实数a的取值范围为{a|-
| 13 |
| 5 |
点评:本题考查了集合的化简与集合的运算的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将3张不同的奥运门票分给10名同学中的3人,每人1张,则不同的分法有( )
| A、2610种 | B、720种 |
| C、240种 | D、60种 |
下列函数中,在其定义域上为奇函数的是( )
| A、y=ex+e-x | ||
B、y=-
| ||
| C、y=tan|x| | ||
D、y=ln
|
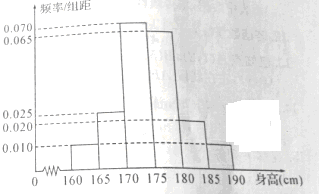 为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.
为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.