题目内容
11.已知点A(0,3),B(3,0),如果抛物线y=x2-ax+a+1与线段AB(不包括线段端点A,B)有两个不同的交点,求a满足的条件.分析 由题意可求线段AB所在的直线的解析式为y=-x+3(0≤x≤3),由抛物线与线段所在的线段y=-x+3(0≤x≤3)有两个不同的交点,可得方程x2+(1-a)x+a-2=0,在[0,3]上应该有两个不相等的实数根即f(x)=x2+(1-a)x+a-2在[0,3]与x轴上有2个交点,结合二次函数的性质得不等式组,解出即可.
解答 解:设线段AB所在的直线的解析式为y=kx+b,
分别把(3,0),(0,3)代入可得,0=3k+b,3=b
解得k=-1,b=3,
∴线段AB所在的直线的解析式为y=-x+3(0≤x≤3),
联立y=-x+3,y=x2-ax+a+1,得x2+(1-a)x+a-2=0,
因为抛物线与线段所在的线段y=-x+3(0≤x≤3)有两个不同的交点,
所以方程x2+(1-a)x+a-2=0,在[0,3]上应该有两个不相等的实数根
令f(x)=x2+(1-a)x+a-2,
∴$\left\{\begin{array}{l}{△{=(1-a)}^{2}-4(a-2)>0}\\{0<\frac{a-1}{2}<3}\\{f(0)=a-2≥0}\\{f(3)=9+3(1-a)+a-2≥0}\end{array}\right.$,
∴2≤a≤5且a≠3.
点评 本题主要考查了直线与曲线的相交关系的应用,解题中要注意解题中的x的范围限制.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
2.若cos2α=$\frac{\sqrt{2}}{3}$,则sin4α+cos4α的值为( )
| A. | 1 | B. | $\frac{7}{9}$ | C. | $\frac{11}{18}$ | D. | $\frac{13}{18}$ |
19.方程x+lgx=3的解x0∈( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
6.一质点的运动方程为s=6t-t2,则在t=2s末的瞬时速度为( )
| A. | 4 | B. | 1 | C. | 2 | D. | 8 |
16.若x0是函数 f(x)=lgx+x-2的一个零点,则x0属于区间( )
| A. | (0,1) | B. | (1,1.5) | C. | (1.5,2) | D. | (2,2.5) |
3.抛物线y=x2与直线x=0、x=1及该抛物线在x=t(0<t<1)处的切线所围成的图形面积的最小值为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
1.已知函数y=Asin(ωx+φ)(x∈R)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则( )
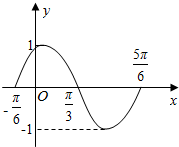

| A. | y=sin(x-$\frac{π}{6}$) | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=-sin(2x+$\frac{π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |