题目内容
1.已知函数y=Asin(ωx+φ)(x∈R)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则( )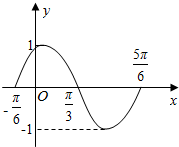
| A. | y=sin(x-$\frac{π}{6}$) | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=-sin(2x+$\frac{π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |
分析 利用函数的周期排除选项,利用特殊角的三角函数值判断即可.
解答 解:由函数的图象可知:函数的周期为:π,所以A不正确;
x=0时,y>0,显然C不正确;
x=-$\frac{π}{6}$时,y=0,y=sin(2x+$\frac{π}{3}$)=0,B正确;
y=sin(2x+$\frac{π}{6}$)≠0,D不正确;
故选:B.
点评 本题考查三角函数的解析式的求法,利用函数的图象排除选项方法比较简洁.

练习册系列答案
相关题目
12.下列各组函数中,表示相同的函数的是( )
| A. | f(x)=x与g(x)=$\frac{{x}^{2}}{x}$ | B. | f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$ | ||
| C. | f(x)=x0与g(x)=1 | D. | f(x)=$\sqrt{{x}^{2}-1}$与g(x)=$\sqrt{x-1}$$\sqrt{x+1}$ |
9.下列函数中,导函数是偶函数的是( )
| A. | y=sinx | B. | y=ex | C. | y=lnx | D. | y=cosx-$\frac{1}{2}$ |
16.若复数Z=$\frac{a-1+2ai}{1-i}$所对应的点在第二象限内,则实数a的取值范围是( )
| A. | a>1 | B. | a>$\frac{1}{3}$ | C. | -1<a<$\frac{1}{3}$ | D. | a<1或a>$\frac{1}{3}$ |
6.下列各组向量中,可以作为基底的是( )
| A. | $\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(1,-2)$ | B. | $\overrightarrow{e_1}=(-1,2),\overrightarrow{e_2}=(5,7)$ | ||
| C. | $\overrightarrow{e_1}=(3,5),\overrightarrow{e_2}=(6,10)$ | D. | $\overrightarrow{e_1}=(\frac{1}{2},-\frac{3}{4}),\overrightarrow{e_2}=(2,-3)$ |
10.在△ABC中,A=60°,AB=2,且△ABC的面积为2$\sqrt{3}$,则BC边的长为( )
| A. | $\sqrt{7}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{7}$ | D. | 7 |