题目内容
 已知三角形的三边为a,b,c,设p=
已知三角形的三边为a,b,c,设p=| 1 |
| 2 |
(1)三角形的面积S=
| p(p-a)(p-b)(p-c) |
(2)r为三角形内切圆的半径,则r=
|
(3)把边BC,CA,AB上的高分别记为ha,hb,hc,则.
ha=
| 2 |
| a |
| p(p-a)(p-b)(p-c) |
| 2 |
| b |
| p(p-a)(p-b)(p-c) |
| 2 |
| c |
| p(p-a)(p-b)(p-c) |
考点:余弦定理,正弦定理
专题:计算题,解三角形
分析:(1)设三角形的三边a、b、c的对角分别为A、B、C,则由余弦定理可得cosC=
,代入三角形面积公式S=
absinC,设p=
,则p-a=
,p-b=
,p-c=
,即可化简得证.
(2)由(1)可得S=
.而又因为S=
,结合上述两式即可得证.
(3)由三角形面积公式可得S=
=
aha=
bhb=
chc,即可得解.
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
| a+b+c |
| 2 |
| -a+b+c |
| 2 |
| a-b+c |
| 2 |
| a+b-c |
| 2 |
(2)由(1)可得S=
| p(p-a)(p-b)(p-c) |
| r(a+b+c) |
| 2 |
(3)由三角形面积公式可得S=
| p(p-a)(p-b)(p-c) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)设三角形的三边a、b、c的对角分别为A、B、C,则由余弦定理可得:
cosC=
,
S=
absinC
=
ab
=
ab
=
=
=
=
,①
设p=
,
则p-a=
,p-b=
,p-c=
,
上式①=
=
.
所以,三角形的面积S=
.
(2)根据海伦公式:三角形的面积S=
.
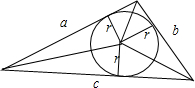
而又因为S=
ar+
br+
cr=
(如下图所示),
结合上述两式:r=
,证毕.
(3)∵边BC,CA,AB上的高分别记为ha,hb,hc,三角形的面积S=
.
∴S=
=
aha=
bhb=
chc.
∴可解得:ha=
,hb=
,hc=
.
cosC=
| a2+b2-c2 |
| 2ab |
S=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1-cos2C |
=
| 1 |
| 2 |
1-
|
=
| 1 |
| 4 |
| 4a2b2-(a2+b2-c2)2 |
=
| 1 |
| 4 |
| (2ab+a2+b2-c2)(2ab-a2-b2+c2) |
=
| 1 |
| 4 |
| [(a+b)2-c2][c2-(a-b)2] |
=
| 1 |
| 4 |
| (a+b+c)(a+b-c)(a-b+c)(-a+b+c) |
设p=
| a+b+c |
| 2 |
则p-a=
| -a+b+c |
| 2 |
| a-b+c |
| 2 |
| a+b-c |
| 2 |
上式①=
|
| p(p-a)(p-b)(p-c) |
所以,三角形的面积S=
| p(p-a)(p-b)(p-c) |
(2)根据海伦公式:三角形的面积S=
| p(p-a)(p-b)(p-c) |
而又因为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| r(a+b+c) |
| 2 |

结合上述两式:r=
|
(3)∵边BC,CA,AB上的高分别记为ha,hb,hc,三角形的面积S=
| p(p-a)(p-b)(p-c) |
∴S=
| p(p-a)(p-b)(p-c) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴可解得:ha=
| 2 |
| a |
| p(p-a)(p-b)(p-c) |
| 2 |
| b |
| p(p-a)(p-b)(p-c) |
| 2 |
| c |
| p(p-a)(p-b)(p-c) |
点评:本题主要考查了余弦定理、三角形面积公式,平方差公式的应用,计算量较大,属于中档题.

练习册系列答案
相关题目
把函数y=cos(x+
π)的图象向右平移φ(φ>0)个单位,所得到的函数图象正好关于y轴对称,则φ的最小值为( )
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设a=30.3,b=0.33,c=log30.3的大小关系是( )
| A、a<b<c |
| B、b<c<a |
| C、c<b<a |
| D、c<a<b |
不等式x2-2x-3<0的解集是( )
| A、(-3,1) |
| B、(-1,3) |
| C、(-∞,-1)∪(3,+∞) |
| D、(-∞,-3)∪(1,+∞) |
下列命题中,真命题是( )
| A、?x0∈R,|x0|≤0 | ||
B、a-b=0的充要条件是
| ||
| C、?x∈R,2x>x2 | ||
| D、若p∧q为假,则p∨q为假(p,q是两个命题) |