题目内容
6.已知函数f(x)=2sinx-3x,若对任意m∈[-2,2],f(ma-3)+f(a2)>0的恒成立,则a的取值范围是( )| A. | (-1,1) | B. | (-∞,-1)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(1,+∞) |
分析 先利用定义、导数分别判断出函数的奇偶性、单调性,然后利用函数的性质可去掉不等式中的符号“f”,转化具体不等式,借助一次函数的性质可得a的不等式组,解出可得答案.
解答 解:∵f(-x)=2sin(-x)-3(-x)=-(2sinx-3x)=-f(x),
∴f(x)是奇函数,
又f'(x)=2cosx-3<0,∴f(x)单调递减,
f(ma-3)+f(a2)>0可化为f(ma-3)>-f(a2)=f(-a2),
由f(x)递减知ma-3<-a2,即ma+a2-3<0,
∴对任意的m∈[-2,2],f(ma-3)+f(a2)>0恒成立,
等价于对任意的m∈[-2,2],ma+a2-3<0恒成立,
则$\left\{\begin{array}{l}{-2a+{a}^{2}-3<0}\\{2a+{a}^{2}-3<0}\end{array}\right.$,解得-1<a<1,
故选:A.
点评 本题考查恒成立问题,考查函数的奇偶性、单调性的应用,考查转化思想,考查学生灵活运用知识解决问题的能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
(1)求y关于t的回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$
(2)用所求回归方程预测该地区2016年(t=6)的人民币储蓄存款.
附:回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中,
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}=\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}}\\{a=\overline{y}-b\overline{t}}\end{array}\right.$.
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(2)用所求回归方程预测该地区2016年(t=6)的人民币储蓄存款.
附:回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中,
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}=\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}}\\{a=\overline{y}-b\overline{t}}\end{array}\right.$.
11.已知函数f(x)=$\left\{\begin{array}{l}{3{x}^{2}-x,x≤2}\\{\frac{1}{2-x},x>2}\end{array}\right.$,则f(f(-3))的值为( )
| A. | $\frac{1}{32}$ | B. | -$\frac{1}{28}$ | C. | $\frac{1}{28}$ | D. | -$\frac{1}{32}$ |
18.已知集合A={x|x2<4},B={x∈Z|-3≤x<1},则A∩B=( )
| A. | {-2,-1,0} | B. | (-1,0) | C. | {-1,0} | D. | (-3,-2) |
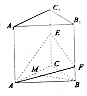 如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.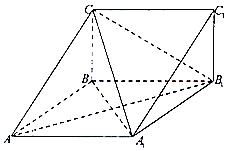 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.