题目内容
16.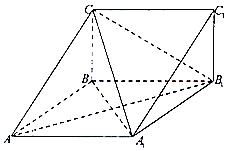 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3.(1)求证:BC∥平面A1B1C1;
(2)求证:AB1⊥平面A1BC;
(3)求三棱锥C-A1B1C1的体积.
分析 (1)证明BC∥B1C1,然后证明BC∥平面A1B1C1.
(2)证明CB⊥AB.CB⊥BB1,推出CB⊥面AA1B1B,得到CB⊥AB1,然后证明AB1⊥A1B,即可证明AB1⊥面A1BC.
(3)过B作BD⊥A1B1于D,说明BD⊥面AA1B1B,然后求解几何体的体积即可.
解答 解:(1)证明:∵四边形BCC1B1为矩形,
∴BC∥B1C1,
∵BC?平面A1B1C1,B1C1?平面A1B1C1,
∴BC∥平面A1B1C1.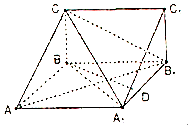
(2)证明:在△ABC中AC=5,AB=4,BC=3,
满足AC2=AB2+BC2,所以∠ABC=90°,即CB⊥AB.
又因为四边形BCC1B1为矩形,所以CB⊥BB1,
又$\left\{\begin{array}{l}CB⊥B{B_1}\\ CB⊥AB\\ B{B_1}?面A{A_1}{B_1}B\\ AB?面A{A_1}{B_1}B\\ B{B_1}∩AB=B\end{array}\right.$,所以CB⊥面AA1B1B,
又因为AB1?面AA1B1B,所以CB⊥AB1,
又因为四边形A1ABB1为菱形,所以AB1⊥A1B,
又$\left\{\begin{array}{l}A{B_1}⊥CB\\ A{B_1}⊥{A_1}B\\ CB?面{A_1}BC\\{A_1}B?面{A_1}BC\\ CB∩{A_1}B=B\end{array}\right.$,所以AB1⊥面A1BC.
(3)解:过B作BD⊥A1B1于D,
由第(1)问已证CB⊥面AA1B1B,
∴C1B1⊥面AA1B1B,
∴C1B1⊥BD,
∴BD⊥面AA1B1B,
由题设知$BD=2\sqrt{2}$,
∴${V_{锥C-{A_1}{B_1}{C_1}}}=\frac{1}{3}×\frac{1}{2}{A_1}{B_1}•{B_1}{C_1}•BD=\frac{1}{3}×\frac{1}{2}×4×3×2\sqrt{2}$=$4\sqrt{2}$.
∴三棱锥C-A1B1C1的体积是$4\sqrt{2}$.
点评 本题考查直线与平面平行、直线与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象能力逻辑推理能力以及计算能力.

| A. | (-1,1) | B. | (-∞,-1)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(1,+∞) |
| A. | $\frac{π}{2017}$ | B. | $\frac{2π}{2017}$ | C. | $\frac{4π}{2017}$ | D. | $\frac{π}{4034}$ |
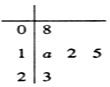 如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )
如图是一名篮球运动员在最近5场比赛中所得分数的茎叶图,若该运动员在这5场比赛中的得分的中位数为12,则该运动员这5场比赛得分的平均数不可能为( )| A. | $\frac{68}{5}$ | B. | $\frac{69}{5}$ | C. | 14 | D. | $\frac{71}{5}$ |
92 89 95 91 93
去掉一个最高分和一个最低分后,所剩数的平均值和方差分别为( )
| A. | 92,4 | B. | 93,5 | C. | 93,4 | D. | 92,$\frac{2}{3}$ |
| A. | 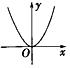 | B. | 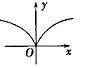 | C. | 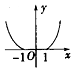 | D. | 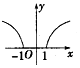 |
 若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为72.
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则这个棱柱的侧面积为72.