题目内容
14.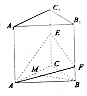 如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.
如图,在三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,倒棱AA1⊥平面ABC,点E,F分别是棱CC1,BB1上的点,且EC=2FB=2.(Ⅰ)若点M是线段AC的中点,证明:
(1)MB∥平面AEF;
(2)平面AEF⊥平面ACC1A1;
(Ⅱ)求三棱锥B-AEF的体积.
分析 (Ⅰ) (1)取线段AE的中点G,连结MG,由三角形中位线定理可得MG=$\frac{1}{2}EC=BF$,又MG∥EC∥BF,可得MBFG是平行四边形,故MB∥FG,由线面平行的判定可得MB∥平面AEF;
(2)由MB⊥AC,平面ACC1A1⊥平面ABC,可得MB⊥平面ACC1A1,进一步得到FG⊥平面ACC1A1.由面面垂直的判定可得平面AEF⊥平面ACC1A1;
(Ⅱ)作AD⊥BC于D,则AD⊥平面BEF,由等积法结合已知求出三棱锥A-BEF的体积得答案.
解答 (Ⅰ)证明:(1)取线段AE的中点G,连结MG,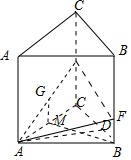
则MG=$\frac{1}{2}EC=BF$,又MG∥EC∥BF,
∴MBFG是平行四边形,故MB∥FG.
而FG?平面AEF,MB?平面AEF,
∴MB∥平面AEF;
(2)∵MB⊥AC,平面ACC1A1⊥平面ABC,
∴MB⊥平面ACC1A1,而BM∥FG,
∴FG⊥平面ACC1A1.
∵FG?平面AEF,∴平面AEF⊥平面ACC1A1;
(Ⅱ)解:作AD⊥BC于D,则AD⊥平面BEF,且AD=$\sqrt{3}$.
于是${V}_{A-BEF}=\frac{1}{3}×{S}_{△BEF}×AD=\frac{1}{3}×\frac{1}{2}×1×2×\sqrt{3}=\frac{\sqrt{3}}{3}$.
故${V}_{B-AEF}={V}_{A-BEF}=\frac{\sqrt{3}}{3}$.
点评 本题考查平面与平面垂直的判定,考查空间想象能力和思维能力,训练了利用等体积法求多面体的体积,属中档题.

练习册系列答案
相关题目
2.已知圆(x+1)2+y2=2,则其圆心和半径分别为( )
| A. | (1,0),2 | B. | (-1,0),2 | C. | (1,0),$\sqrt{2}$ | D. | (-1,0),$\sqrt{2}$ |
9.若tanα=3,则${cos^2}({α+\frac{π}{4}})-{cos^2}({α-\frac{π}{4}})$=( )
| A. | $-\frac{3}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
6.已知函数f(x)=2sinx-3x,若对任意m∈[-2,2],f(ma-3)+f(a2)>0的恒成立,则a的取值范围是( )
| A. | (-1,1) | B. | (-∞,-1)∪(3,+∞) | C. | (-3,3) | D. | (-∞,-3)∪(1,+∞) |
 在三棱锥P-ABC中,△PAB是等边三角形,∠APC=∠BPC=60°.
在三棱锥P-ABC中,△PAB是等边三角形,∠APC=∠BPC=60°.