题目内容
6.已知函数f(x)=lnx-ax.其中a为非零常数.(1)求a=1时,f(x)的单调区间;
(2)设b∈R,若f(x)≤b-a对x>0恒成立,求$\frac{b}{a}$的最小值.
分析 (1)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)根据f(x)≤b-a?b>lnx-ax+a,设h(x)=lnx-ax+a,通过讨论a的范围,求出h(x)的最大值,从而求出$\frac{b}{a}$的最小值即可.
解答 解:(1)a=1时,f(x)=lnx-x,则f′(x)=$\frac{1}{x}$-1,
0<x<1时,f′(x)>0,x>1时,f′(x)<0,
∴f(x)在(0,1)递增,在(1,+∞)递减;
(2)f(x)≤b-a?b>lnx-ax+a,
设h(x)=lnx-ax+a,则h′(x)=$\frac{1}{x}$-a,
a<0时,h′(x)>0,h(x)在(0,+∞)递增,b≥h(x)不可能恒成立,
a>0时,h′(x)>0?0<x<$\frac{1}{a}$,h′(x)<0?x>$\frac{1}{a}$,
∴h(x)max=h($\frac{1}{a}$)=ln($\frac{1}{a}$)-1+a=a-lna-1,
b≥a-lna-1?$\frac{b}{a}$≥1-$\frac{lna}{a}$-$\frac{1}{a}$,
设g(a)=1-$\frac{lna}{a}$-$\frac{1}{a}$(a>0),g′(a)=$\frac{lna}{{a}^{2}}$,
∴g′(a)>0?a>1,g′(a)<0?0<a<1,
∴g(x)min=g(1)=0,解得:$\frac{b}{a}$≥0,
∴a=1,b=0时,$\frac{b}{a}$取最小值0.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、转化思想,是一道中档题.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
15.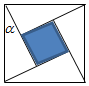 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
( )
 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
| A. | $1-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{4-\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
16.设θ∈R,“sinθ=cosθ“是“cos2θ=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |