题目内容
以直角坐标系的原点O为极点，x轴的正半轴为极轴．已知点P的直角坐标为（1，-5），点M的极坐标为（4，
）．若直线L过点P，且倾斜角为
，圆C以M为圆心、4为半径．则直线L的参数方程是 ，圆C的极坐标方程是 ．
| π |
| 2 |
| π |
| 3 |
考点：直线的参数方程,简单曲线的极坐标方程
专题：坐标系和参数方程
分析：由直线的参数方程和圆的极坐标方程可得答案．
解答：
解：由题意可得直线l的参数方程为
，（t为参数）
圆C的极坐标方程为ρ=8sinθ，
故答案为：
，ρ=8sinθ
|
圆C的极坐标方程为ρ=8sinθ，
故答案为：
|
点评：本题考查直线的参数方程，圆的极坐标方程，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若（2+2i）（1-mi）（i为虚数单位）为纯虚数，则实数m的值等于（ ）
| A、1 | B、-1 | C、0 | D、1或-1 |
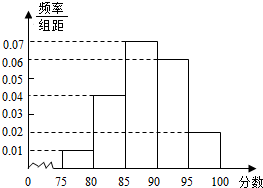某工厂招聘工人，在一次大型的招聘中，其中1000人的笔试成绩的频率分布直方图如图所示，按厂方规定85分以上（含85分）可以直接录用．