题目内容
3．如图，四面体ABCD被一平面所截，截面EFHG是一个平行四边形．求证：CD∥GH．
分析 先根据四边形EFGH为平行四边形得到EF∥GH，进而可根据线面平行的判定定理可证明EF∥平面BCD，再由线面平行的性质定理可得到EF∥CD，从而得证CD∥GH．
解答 证明：∵四边形EFGH为平行四边形，
∴EF∥GH．又GH?平面BCD，
∴EF∥平面BCD．
而平面ACD∩平面BCD=CD，EF?平面ACD，
∴EF∥CD，∴CD∥GH．
点评 本题考查线线平行的证明，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
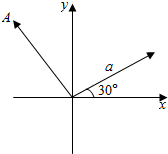如图，点A的坐标为（-2，3），向量$\overrightarrow{a}$的模为4，则向量$\overrightarrow{OA}$的坐标为（-2，3），向量$\overrightarrow{a}$的坐标为（2$\sqrt{3}$，2）．
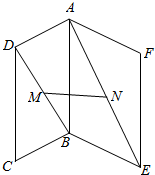如图，边长相等的两个正方形ABCD和ABEF所在平面相交于AB，M∈BD，N∈AE且BM=EN≠BD．求证：MN⊥AB．
17．数列{an}满足a1=1，对任意的n∈N*都有an+1=a1+an+n，则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2016}}}}$=（ ）
| A． | $\frac{2015}{2016}$ | B． | $\frac{2016}{2017}$ | C． | $\frac{4032}{2017}$ | D． | $\frac{4034}{2017}$ |