题目内容
一辆汽车在行驶中由于遇到紧急情况而刹车,以速度v(t)=7-3t+
(t的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是 .
| 25 |
| 1+t |
考点:变化的快慢与变化率
专题:导数的综合应用
分析:令v(t)=0,解得t=4,则所求的距离S
(7-3t+
)dt,解出即可.
| ∫ | 4 0 |
| 25 |
| 1+t |
解答:
解:解:令v(t)=)=7-3t+
=0化为3t2-4t-32=0,又t>0,解得t=4.
∴由刹车行驶至停止,在此期间汽车继续行驶的距离:
s=
(7-3t+
)dt=[7t-
+25ln(1+t)]
=4+25ln5,
故答案为:4+25ln5
| 25 |
| 1+t |
∴由刹车行驶至停止,在此期间汽车继续行驶的距离:
s=
| ∫ | 4 0 |
| 25 |
| 1+t |
| 3t2 |
| 2 |
| | | 4 0 |
故答案为:4+25ln5
点评:熟练掌握导数的运算法则和定积分的几何意义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在钝角△ABC中,“sinA=
”是“∠A=
”的( )
| ||
| 2 |
| 2π |
| 3 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
已知向量
,
的夹角为120°,且|
|=1,|
|=2,则向量
-
在向量
+
上的投影是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、-
| ||||
B、
| ||||
C、
| ||||
| D、-3 |
函数f(x)=-x2+2(a-1)x+2在(-∞,4)上是增函数,则实数a的范围是( )
| A、a≤-3 | B、a≤5 |
| C、a≥3 | D、a≥5 |
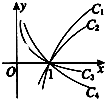 已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为
已知函数C1:y=logax,C2=y=logbx,C3:y=logcx,C4:y=logdx在同一平面直角坐标系中的图象如图所示,其中a、b、c、d均为不等于1的整数,则a、b、c、d、1按从大到小的顺序为