题目内容
14.在△ABC中,下列各表达式为常数的是( )| A. | sin(A+B)+sinC | B. | cos(A+B)-cosA | C. | sin2$\frac{A+B}{2}$+sin2$\frac{C}{2}$ | D. | sin$\frac{A+B}{2}$sin$\frac{C}{2}$ |
分析 由三角形的内角和定理结合三角函数的诱导公式逐一分析四个选项得答案.
解答 解:在△ABC中,∵A+B+C=π,
∴A、sin(A+B)+sinC=2sinC,不为常数;
B、cos(A+B)-cosA=-cosC-cosA,不为常数;
C、sin2$\frac{A+B}{2}$+sin2$\frac{C}{2}$=cos2$\frac{C}{2}$+sin2$\frac{C}{2}$=1,为常数;
D、sin$\frac{A+B}{2}$sin$\frac{C}{2}$=cos$\frac{C}{2}$sin$\frac{C}{2}$=$\frac{1}{2}$sinC,不为常数.
故选:C.
点评 本题考查了三角函数的化简求值,考查了三角函数的诱导公式,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
4.已知α,β∈(0,$\frac{π}{2}$),且cosα=$\frac{4}{5}$,cos(α+β)=-$\frac{4}{5}$,则cosβ等于( )
| A. | $\frac{4}{25}$ | B. | $-\frac{4}{25}$ | C. | $\frac{7}{25}$ | D. | $-\frac{7}{25}$ |
5.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}(x∈[0,+∞))}\\{{a}^{x}+{a}^{2}-3a+1(x∈(-∞,0))}\end{array}\right.$在区间(-∞,+∞)是增函数,则常数a的取值范围是( )
| A. | 1≤a≤2 | B. | a<1或a≥2 | C. | 1<a≤2 | D. | a<1或a>2 |
6.已知A,B两地间的距离为20km,B,C两地间的距离为40km,现测得∠ABC=120°,则A,C两地间的距离为( )
| A. | 20km | B. | 20$\sqrt{3}$km | C. | 20$\sqrt{5}$km | D. | 20$\sqrt{7}$km |
3.设函数f(x)=$\left\{\begin{array}{l}{{2}^{-x}}&{x<0}\\{1+2x}&{x≥0}\end{array}\right.$,则f(2)-f(-2)的值是( )
| A. | -$\frac{11}{4}$ | B. | 1 | C. | $\frac{19}{4}$ | D. | $\frac{21}{4}$ |
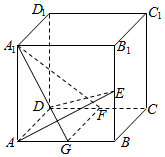 如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.
如图在正方体ABCD-A1B1C1D1中,E为BB1的中点,F为CD的中点,G为AB的中点.求证:平面AED⊥平面A1FG.